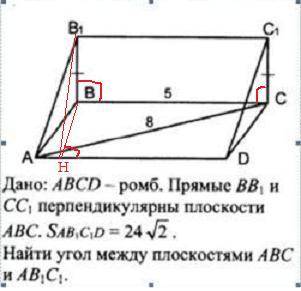
АВСD -ромб, АВ=5 , АС=8 , ВВ₁⊥(АВС), СС₁⊥(АВС), ВВ₁=СС₁ , S(АВ₁С₁D)=24√2 .
Найти угол между плоскостями (АВС) и(АВ₁С₁)
Объяснение:
Пусть ВН⊥AD, тогда В₁Н⊥AD по т. о 3-х перпендикулярах, а значит угол ∠В₁НВ-линейный угол между плоскостями (АВС) и(АВ₁С₁).
1)По св.диагоналей ромба из прямоугольного ΔАОВ найдем ВО=√(5²-4²)=3, ВD=6 . S(роба)=1/2*d₁*d₂ , S(роба)=1/2*48=24.
С другой стороны S(ромба)=a*h или 24=5*ВН , ВН=4,8 .
2)АВ₁С₁D-параллелограмм ( **), его S(АВ₁С₁D)=24√2 , AD=5 , тогда В₁Н=24√2:5=4,8√2.
3)ΔВВ₁Н-прямоугольный cos∠В₁НВ=ВН/В₁Н или cos∠В₁НВ=4,8/4,8√2=1/√2=√2/2 ⇒ ∠В₁НВ=45°
PS(**)
АВВ₁=ΔDCC₁ , как прямоугольные по двум катетам АВ=СD ,ВВ₁=СС₁. В равных треугольниках соответственные элементы равны ⇒ АВ₁=DС₁.
По признаку параллелограмма ( о равенстве противоположных сторон) -АВ₁С₁D параллелограмм.
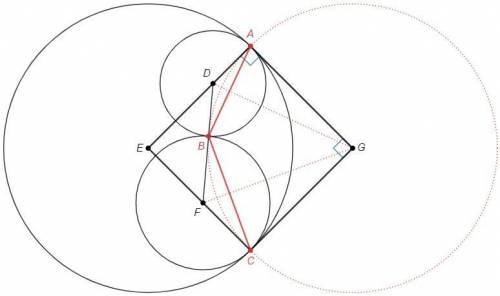
Центр G описанной окружности △ABC лежит на пересечении серединных перпендикуляров к сторонам AB и BC. Серединный перпендикуляр к хорде является биссектрисой центрального угла. DG - биссектриса ADB, FG - биссектриса BFC. Точка G является пересечением биссектрис внешних углов △DEF и центром вневписанной окружности.
EA=EC, DA=DB, FC=FB (радиусы)
ED+DA=EF+FC => ED+DB=EF+FB
Точка B делит периметр △DEF пополам, следовательно является точкой касания вневписанной окружности.
GB - радиус вневписанной окружности △DEF, следовательно GA также радиус этой окружности, A - точка касания. Радиус в точку касания перпендикулярен касательной, A=90.
EAGC - ромб (стороны равны как радиусы равных окружностей) с прямым углом A, следовательно квадрат, G=90.
∪AC=90, ∪CA=360-90=270, ABC=270/2=135
Объяснение:
НВ равна 18 сантиметра нужно найти просто все углы и идти через свойство про гипотенузу