Так как отрезки РР₁ и ММ₁ перпендикулярны плоскости а, то указанные отрезки лежат на одной плоскости, а точка Р₁ лежит на отрезке КМ₁.
Рассмотрим ∆КРР₁ и ∆КММ₁.
Угол МКМ₁ – общий;
Угол КР₁Р=угол КМ₁М (оба прямые, так как РР₁ и ММ₁ перпендикулярны КМ₁)
Следовательно ∆КРР₁~∆КММ₁ по двум углам.
Пусть КР=n, тогда РМ=2n (из отношения КР:РМ=1:2), следовательно КМ=KP+PM=n+2n=3n.
Отношение двух любых сторон одного треугольника, равно отношению двух соответствующих сторон треугольника, подобного первому. Тогда:
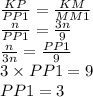
ответ: 3 см
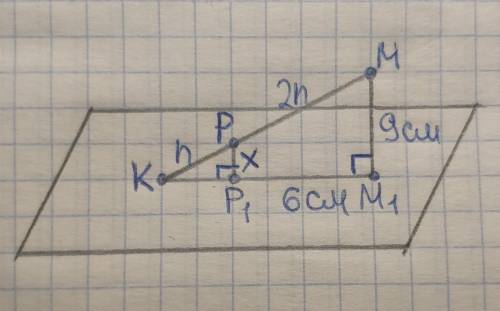
1) Пусть имеем треугольник ABC, BH- высота,тогда
AH=HC=AC/2=8/2=4
Из прямоугольного треугольника HBC по теореме Пифагора получим
(BC)^2=(HC)^2+(BH)^2
(BC)^2=16+9=25
BC=5
2) P=40 => сторона ромба=40/4=10
AC и BD - диагонали ромба
точка О - точка пересечения диагоналей
Угол BAO=30 градусов
Сторона лежащая в прямоугольном треугольнике против угла 30 градусов равна половине гипотенузы, то есть BO=AB/2=10/2=5 и диагональ BD=2*5=10
Из треугольника AB0 по теореме Пифагора
(AO)^2=(AB)^2-(BO)^2
(AO)^2=100-25=75
AO=5√3 и диагональ AC=2*5√3=10√3
S=d1*d2/2
S=10*10√3/2=50√3
имеем равнобедренный треугольник MKC (по усл.)
∠MKC равен 48° (по усл.)
Значит ∠M = 48°
∠MKO = 84 ÷ 2 = 42°
∠MOK = 180 - (∠OMK + ∠MKO) = 180 - (48 + 42) = 90°
ответ: ∠OMK = 48°, ∠MKO = 42°, ∠MOK = 90°
удачи получить пять! ;)