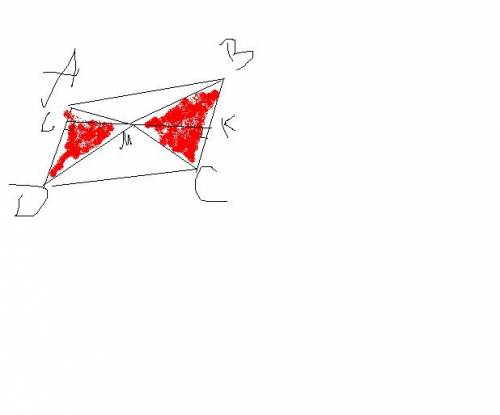
проведем через точку М, пряммую перпендикулярную АD, так как AD||BC, то она будет перпендикулярна и прямой ВС, пусть пряммую AD она пересекает в точке L, а пряммую BC в точке K.
Тогда LM - высота параллелограмма ABCD, LM - высота треугольника ADM, KM - высота треугольника BCM.
Площадь парарлелограмма равна произведению его стороны на высоту, проведенную к этой стороне
Площадь треугольника равна половине произведения стороны на высоту провдеенной к этой стороне
Поэтому
S(AMD)+S(BMC)=1/2*AD*LM+1/2*BC*KM=так противоположные стороны парарлелограмма равны=
=1/2*AD*LM+1/2*AD*KM=1/2*AD*(LM+KM)=1/2*AD*LK=1/2*S(ABCD), что и требовалось доказать
1. Отрезок FK пересекает прямую РМ
2. При пересечении двух прямых, образуются смежные, а также вертикальные углы. Смежные углы это те, которые на одной прямой, а прямая у нас 180°. Поэтому, мы от 180° отнимаем известный нам угол (58°), находим смежный ему угол (122°). Остальные углы они являются вертикальными по отношению к этим. Поэтому, тот угол, который напротив угла в 58° равен 58°. А тот который напротив 122°,равен 122°.
3. K-середина отрезка CD, то следует что CK и KD равны, а значит 8:2=4см--CK, KD. CM=MK то 4:2=2см--CM,MK. ответ: CM=2cm; MK=2cm; KD=8cm.
Объяснение: