В прямоугольнике ABCD диагонали пересекаются в точке О. Угол COD равен 32°. Найдите углы ODA, OAB, BOC, BOA.
- - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - -
Дано :
Четырёхугольник ABCD - прямоугольник.
АС∩BD = O.
∠COD = 32°.
Найти :
∠ODA = ?
∠ОАВ = ?
∠ВОС = ?
∠ВОА = ?
∠ВОА = ∠COD = 32° (так как вертикальные).
∠ВОС + ∠COD = 180° (так как смежные) ⇒ ∠ВОС = 180° - ∠COD = 180° - 32° = 148°.
Диагонали прямоугольника равны и точкой пересечения делятся пополам.Следовательно, АО = ВО = СО = DO.
Рассмотрим ΔCOD - равнобедренный (по определению).
По теореме о сумме углов треугольника - ∠COD + ∠OCD + ∠ODC = 180° ⇒ ∠OCD + ∠ODC = 180° - ∠COD = 180° - 32° = 148°.
Учитываем, что углы при основании равнобедренного треугольника равны - ∠ODC = ∠OCD = 148° : 2 = 74°.
Тогда ∠ODA + ∠ODC = 90° ⇒ ∠ODA = 90° - ∠ODC = 90° - 74° = 16°.
Рассмотрим ΔВОА - равнобедренный (по определению).
По теореме о сумме углов треугольника - ∠ВОА + ∠ОАВ + ∠ОВА = 180° ⇒ ∠ОАВ + ∠ОВА = 180° - ∠ВОА = 180° - 32° = 148°.
Учитываем, что углы при основании равнобедренного треугольника равны - ∠ОАВ = ∠ОВА = 148° : 2 = 74°.
∠ODA = 16°, ∠ОАВ = 74°, ∠ВОС = 148°, ∠ВОА = 32°.
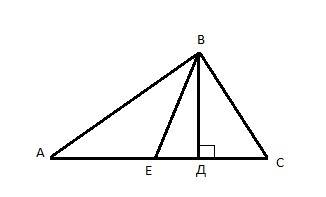
Построим произвольный прямоугольный треугольник АВС. Проведем из прямого угла АВС высоту ВД и медиану ВЕ.
Наибольшим углом данного треугольника будет ∠АВС=90 градусам.
Найдем наибольший ОСТРЫЙ угол данного треугольника:
По условию ∠ДВЕ=3 °.
Рассмотрим треугольник ВДЕ:
∠ВЕД=180-ВДЕ-ДВЕ=180-90-3=87 °.
∠ВЕА=180-ВЕД=180-87=93 °(как смежные углы).
Так как медиана, проведенная из вершины прямого угла, равна половине гипотенузы мы получаем два равнобедренных треугольника:
ВАЕ и ВСЕ
Рассмотрим треугольник ВАЕ:
так как АЕ=ВЕ то углы ВАЕ=АВЕ (углы при основании равнобедренного треугольника)
Значит ∠ВАЕ=(180-ВЕА)/2=(180-93)/2=43,5°
Рассмотрим треугольник ВСЕ:
так как СЕ=ВЕ то углы ВСЕ=СВЕ (углы при основании равнобедренного треугольника)
Значит ∠ВСЕ=(180-ВЕС)/2=(180-87)/2= 46,5°
43,5<46,5
А значит, наибольшим острым углом треугольника АВС является угол ВСА=46,5 градуса
AD=DB=9
CD+4=DB
CD=5
AB=18
S=45
DB•CD•1/2=22.5
Поэтому CDделит триугодник в отнашение 1/2
Объяснение: