Проведём высоту к основанию конуса, и рассмотрим его осевое сечение - это р / б треугольник: диаметр основания это основание,а две образующие ,выходящие из концов данного диаметра - боковые стороны.
Высота конуса совпадает с высотой р/б треугольника , и делит его на два равных прямоугольных треугольника.
Рассмотрим один из них:
Один из катетов равен половине диаметра(радиусу) основания цилиндра 9см.
Гипотенуза это образующая конуса.
Угол между катетом в 9см и гипотенузой равен 30*.
Второй катет совпадает с высотой р/б треугольника(конуса).
Косинус — есть отношение прилежащего катета к гипотенузе.
Синус — есть отношение противолежащего катета к гипотенузе
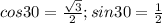
Найдём гипотенузу через косинус:
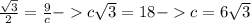
Найдём высоту через синус
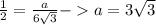
Высота равнобедренного треугольника, проведённая с ВЕРШИНЫ равнобедренного является также и биссектрисой и делит угол при вершине на два одинаковых угла (β/2). Тогда угол при основании равен (90°-β/2) -по свойству острых углов прямоугольного треугольника.
Рассмотрим треуг. с катетом h (данная в условии высота), гипотенузой, которая есть основанием данного равнобедренного треугольника. Гипотенуза прямоугольного треугольника равняется отношению катета к синусу противолежащего угла, тогда основание =h/(sin(90°-β/2)) =h/cos(β/2)
ответ:
h/cos(β/2)