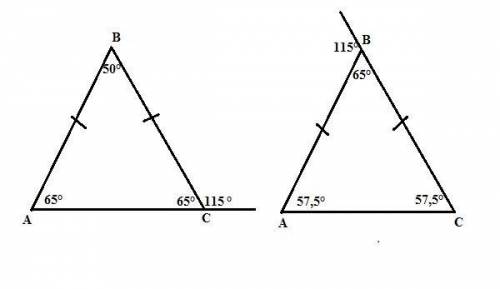
1. 65°, 65°, 50°.
2. 57,5°; 57,5°; 65°.
Объяснение:
Нам дан один из внешних углов равнобедренного треугольника. У равнобедренного треугольника углы при основании равны.
Значит возможны два варианта решения:
1. Если дан внешний угол при основании, то внутренний, смежный с ним, равен 180° - 115° = 65° (сумма смежных углов равна 180°).
Тогда угол при вершине треугольника равен 180° - 2·65° = 50° (по сумме внутренних углов треугольника, равной 180°).
ответ: 65°, 65°, 50°.
2. Если дан внешний угол при вершине, то внутренний, смежный с ним, равен 180° - 115° = 65° (сумма смежных углов равна 180°).
Внешний угол треугольника равен сумме двух внутренних (в нашем случае равных), не смежных с ним углов. Следовательно, углы при основании такого треугольника равны 115°:2 = 57,5°.
ответ: 57,5°; 57,5°; 65°.
1))). Если луч есть биссектриса угла, то любая точка его равноудалена от сторон этого угла.
2))). Прямую, проходящую через середину отрезка перпендикулярно к нему, называют серединным перпендикуляром к отрезку.
Свойства серединных перпендикуляров треугольника
Каждая точка серединного перпендикуляра к отрезку равноудалена от концов этого отрезка.
Точка пересечения серединных перпендикуляров, проведенных к сторонам треугольника, является центром окружности, описанной около этого треугольника.
3))). 1. Точка пересечения биссектрис треугольника- центр вписанной окружности ;
2. Точка пересечения серединных перпендикуляров треугольника- центр описанной окружности ;
3. Точка пересечения медиан треугольника (медианы треугольника пересекаются в отношении 2:1)
4. Точка пересечения высот треугольника - ортоцентр фигуры (центр вписанной и описанной окружности).
Объяснение:
Объяснение:
1)ΔАВР -равнобедренный, значит ∠АВР=∠АРВ
2)∠СВР=90-∠АВР.
3) В ΔВДР-прямоугольный ∠ДВР=90-∠ВРД учитывая 1) имеем ∠ДВР=90-∠АВР
3) Т.к.∠СВР=∠ДВР, и ВР-их общий луч ( сторона) , то ВР-биссектриса.