Объяснение:
Рассмотрим для начала понятие "равные треугольники".
Равные треугольники - это треугольники, которые мы можем совместить наложением.
Однако, сравнивать треугольники по определению очень трудно.
Для этого собственно и ввели признаки равенства треугольников.
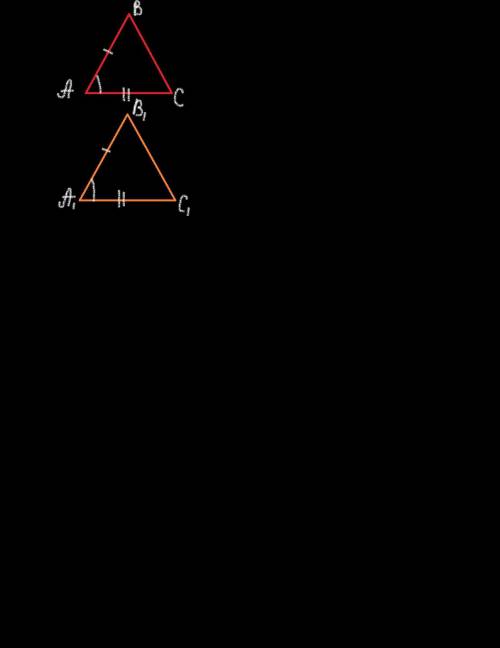
Ну а теперь вспомним доказательство первого признака равенства треугольников(чертежи треугольников прикреплены снизу):
нам даны два треугольника: ABC и A1B1C1
По условию у этих треугольников равны:
стороны AB = A1B1
стороны AC = A1C1
углы A = A1
Если мы совместим треугольники наложением, то эти треугольники совместятся в вершинах AB и A1B1, AC и A1C1, и на углах A и A1.
Получается, что если у треугольников равны две стороны и углы между ними, то они совместятся в этих вершинах при наложении, а следовательно, будут равны.
Мораль сей басни такова: если треугольники равны, то не обязательно у них должны быть все три стороны равны, чтобы они совместились при наложении.
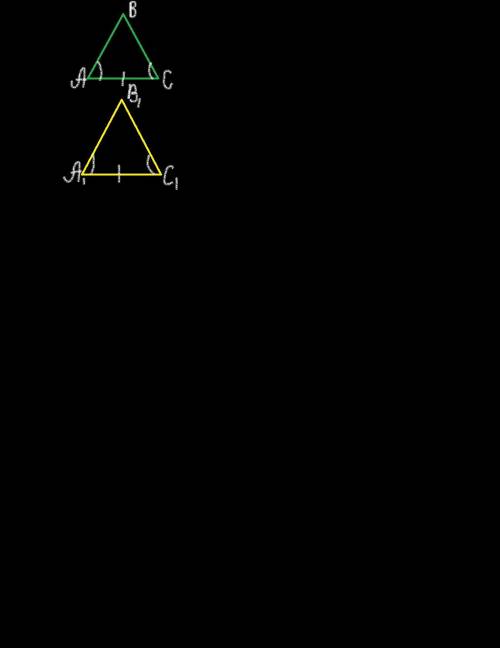
Ну а теперь вспомним второй признак равенства треугольников:
если у треугольников одна сторона и два прилежащих к ней угла равны, то и треугольники равны.
(Чертежи внизу).
Следовательно, если эти треугольники совместить наложением, то они будут равны, так как углы A и A1, C и C1 и стороны AC и A1C1 совместятся.
Еще раз повторю:
Чтобы треугольники совместились при наложении, не обязательно, чтобы равны были все три стороны.
Я смог ответить на твой вопрос? Понятно ли я объяснил?
Высота равностороннего треугольника равна 25√3. Найдите его периметр.
Решение:
1) Так как треугольник равносторонний, то ∠A = ∠B = ∠C = 180° : 3 = 60°.
2) Рассмотрим треугольник ABH (∠H = 90)
∠B = 180° - 90° - 60° = 30°
3) AH = половине AB = AB/2 - Катет, лежащий против угла в 30°.
AB2 = (25√3)2 + (AB/2)2
AB2 = 1875 + AB2/4
AB2 - AB2/4= 1875
(3AB2)/4 = 1875
Крест-накрест:
3AB2 = 4 * 1875
3AB2 = 7500
AB2 = 7500 / 3
AB2 = 2500
AB = √2500
AB = 50
4) Периметр равен сумме всех сторон, так как треугольник имеет 3 стороны и в данном случа они все равны, то:
P = 50 + 50 + 50 = 150
ответ: 150