Объяснение: Для прямоугольных треугольников должна выполняться теорема Пифагора - сумма квадратов катетов = квадрату гипотенузы. Гипотенуза в прямоугольном треугольнике самая большая сторона. Тогда имеем:
2) 11² +20² =? 25² т.е 121 + 400 = 521, 25² = 625. Прямоугольный треугольник такие стороны иметь не может, так как 521 ≠ 625
3) 18² + 24² =? 30² т.е. 324 + 576 = 900, 30² = 900. Такие стороны треугольник может иметь, так как условие теоремы Пифагора 18² + 24² = 30² выполняется.
4) 9² + 12² =? 15², т.е. 81 + 144 = 225, 15² = 225. Такие стороны треугольник может иметь, так как условие теоремы Пифагора 9² + 12² = 15² выполняется.
Условие задачи 1) не ясно. Решить нельзя.
Объяснение:
1) по теореме об угле в 30° в прямоугольном треугольнике CD=1\2AC=4
AC²=AD²+CD²
64=16+AD²
AD²=48 AD=4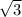
площадь равна AD*CD=16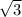
3) опускаем высоту ВЕ, тр-к АВЕ прямоугольный, ∠АВЕ=45°, значит АЕ=ВЕ=8-3=5
площадь= сумме площадей тр-ка АВЕ и пр-ка ВСDЕ=1/2*5*5+3*5=12,5
4) опускаем высоту ВЕ. тр-к АВЕ прямоугольный, ∠АВЕ=30°
по теореме об угле в 30°, АЕ=1\2АВ=2. АВ²=ВЕ²+АЕ² ВЕ=2√3
площадь = 1/2АС*ВЕ=1/2*6*2√3=6√3
5) опускаем высоту из угла В, она делит сторону АС пополам в точке Е
тр-к АВЕ прямоугольный и ВЕ=12.значит площадь тр-ка равна 1/2*ВЕ*АС=108
6) пусть НВ это х, тогда АН=7+х
площадь тр-ка АВС=сумме площадей тр-ков АСН и СНВ
площадь ΔАСН=1/2*12*(7+х)
площадьΔСНВ=1\2*12*х
АВ=х+7+х=2х+7
АС²=(7+х)²+144
ВС²=х²+144
АВ²=(2х+7)²=(х+7)²+144+х²+144
упрощаем х²+7х-144=0
находим корни через дискриминант
один из них отрицательный, другой =5,5
НВ=5,5, АН=12.5, площадьΔАВС=1\2*12*5,5+1/2*12*12,5=108
156 усл.ед.²
Объяснение:
Проведем высоту BH
где a-верхнее основание
b-нижнее основание
h-высота