ответ: А=С=70г.
В=D=110г.(100г.)
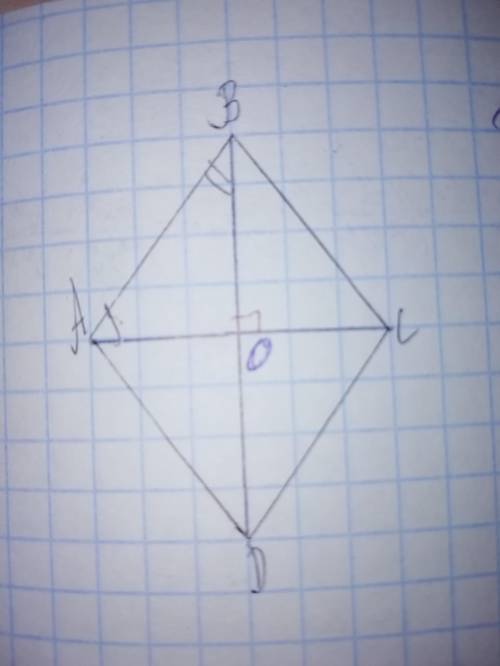
Объяснение: Дано: ABCD - ромб, угол ABO на 20г.(30г.) больше угла BAO.
Найти: углы- А, В, C, D.
Решение: Пусть угол ВАО равен x, по условию угол АВО на 20г.(30г.) больше угла ВАО следовательно угол АВО =x+20. Треугольник АВО - прямоугольный, так как по свойству ромба его диагонали взаимно перпендикулярны, следовательно сумма углов треугольника АВО = 180г. угол АОВ = 90г. Составим уравнение: x+x+20=90
2x=70
x=35
(x+x+30=90; 2x=60; x=30).
угол АВО равен x+20 следовательно угол АВО = 55г. (50г.)
Диагонали ромба являются его биссектрисами (по свойству диагоналей ромба) следовательно угол А = 2ВАО = 70г. угол В = 2АВО =110г.(100г.). По свойству ромба его противоположные углы равны, следовательно угол А = угол С = 70г.
угол В = угол D = 110г.(100г.)
Відповідь:
Окружность (О; r)
∠OBA = 30°
CA — касательная
Найти:
∠BAC — ?
1) Так как радиусы окружности равны, значит, две стороны треугольника ABO равны. ⇒ ΔABO равнобедренный (AO = OB).
У равнобедренного треугольника углы при основании равны, следовательно: ∠OBA = ∠OAB = 30°.
2) Касательная к окружности перпендикулярна радиусу, проведённому в точку касания, значит CA ⊥ OA. ∠OAC = 90°.
3) ∠BAC = ∠OAC - ∠OAB.
∠BAC = 90° - 30° = 60°.
ОТВЕТ: 60°
Быстрое решение (пояснения писать обязательно нужно):
1) ΔABO равнобедренный, так как радиусы окружности, составляющие стороны треугольника, равны (AO = OB). Следовательно, ∠OBA = ∠OAB = 30°.
По свойству касательной, CA ⊥ OA ⇒ ∠OAC = 90°. Значит:
2) ∠BAC = 90° - 30° = 60°
ОТВЕТ: 60°
Пояснення:
Смотри картинку