AC = 12 см, AD/DC = 3/1 ⇒ AD = (3/4)•АС = 9 см, DC = 12 - 9 = 3 см
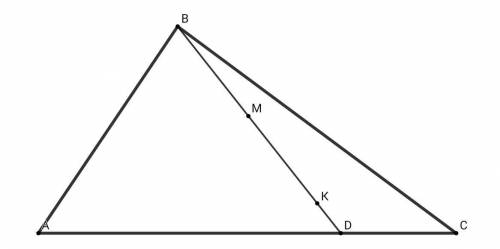
Пусть М и К - это точки касания вписанных окружностей в ΔАВD и ΔBDC соответственно, тогда по известной теореме про значения отрезков касательных:
Отрезок касательной равен разности полупериметра треугольника и противолежащей ей стороны
MD = p₁ - AB и KD = p₂ - BC
p₁ и р₂ - это полупериметры ΔABD и ΔBDC соответственно
Искомое рассстояние MK = MD - KD = p₁ - AB - (p₂ - BC) = p₁ - p₂ + BC - AB = (1/2)•(AB + AD + BD) - (1/2)•(BD + BC + DC) + ВС - АВ = (1/2)•(AD + BC - DC - AB) = (1/2)•(9 + 8 - 3 - 7) = (1/2)•7 = 3,5
Значит, МК = 3,5 см
ответ: 3,5 см
Треугольник ABD — равнобедренный, т.к. его биссектриса BF является высотой Поэтому
AF = FD SAFE = SDFE = 5.
Кроме того BC = 2BD = 2AB. Тогда по свойству биссектрисы треугольника
= 2.
Следовательно,
SDEC = 2SADE = 4SDEF = 20, SADC = 30.
Значит,
SABC = 2SADC = 60.
Треугольник ABD — равнобедренный, т.к. его биссектриса BF является высотой. Поэтому
AF = FD SAFE = SDFE = 5.
Кроме того, BC = 2BD = 2AB. Тогда по свойству биссектрисы треугольника
= 2.
Следовательно,
SDEC = 2SADE = 4SDEF = 20, SADC = 30.
Значит,
SABC = 2SADC = 60.
Треугольник ABD — равнобедренный, т.к. его биссектриса BF является высотой. Поэтому
AF = FD SAFE = SDFE = 5.
Кроме того, BC = 2BD = 2AB. Тогда по свойству биссектрисы треугольника
= = 2.
Следовательно,
SDEC = 2SADE = 4SDEF = 20, SADC = 30.
Значит,
SABC = 2SADC = 60
Даны вершины треугольника А(-2; 1), В(2; 4), С((-2;-2).
1) Векторы АВ = (4; 3), ВС = (-4; -6), АС = (0; -3).
Уравнения (канонические):
АВ: (х + 2)/4 = (у - 1)/3.
ВС: (х - 2)/(-4) = (у - 4)/(-6). Общий вид: 3х -2у + 2 = 0.
АС: (х + 2)/0 = (у - 1)/(-3). Это линия х = -2.
2) Точка М: х(М) = (-2+2-2)/3 = -2/3,
у(М) = (1+4-2)/3 = 1. Точка М((-2/3); 1).
3) Находим уравнение высоты АД из условия А1А2 + В1В2 = 0.
АД: 2х + 3у + С = 0. Подставим координаты точки А:
2*(-2) + 3*1 + С = 0, отсюда С = 4 - 3 = 1.
АД: 2х + 3у + 1 = 0.
Если задано уравнение прямой ВС: Ax + By + C = 0, то расстояние от точки А(Аx, Аy) до прямой ВС можно найти, используя следующую формулу : d = |A·Аx + B·Аy + C| . А(-2; 1).
√(A² + B²) ВС: 3х -2у + 2 = 0.
Подставим данные: d = |3·(-2) + (-2)·1+ 2| =
√(3² + (-2)²)
= |-6 - 2 + 2|/√13 = 6/√13 ≈ 1,664.
4) Так как одна сторона треугольника вертикальна и равна 3, то высота равна разности координат точек по оси Ох, то есть 2 - (-2) = 4.
ответ: S = (1/2)*3*4 = 6.