При пересечении двух прямых образуются только углы двух видов: смежные и вертикальные.
Перпендикулярные прямые рассматривать смысла нет: все углы по 90° и условие не выполняется, поэтому есть 2 тупых и 2 острых угла.
У смежных углов сумма равна 180°.
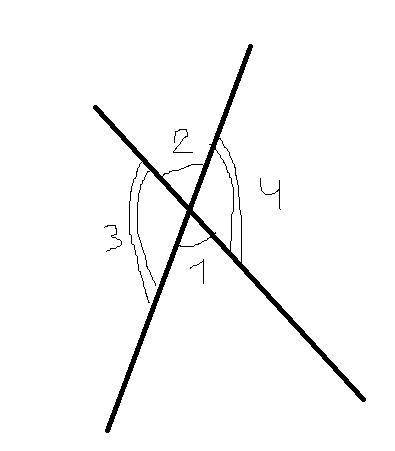
То есть даже на примере:
∠1 смежен с ∠3 и ∠4, то есть ∠1+∠3=180°, ∠1+∠4=180°
Аналогично ∠2 смежен с теми же углами. И ∠1=∠2.
И это явно не могут быть 2 тупых угла, так как они как вертикальные равны между собой, но если ∠3+∠4=140° и ∠3=∠4, то ∠3=∠4=70°, а они тупые, то есть такого быть не может. Поэтому это могут быть только ∠1 и ∠2, которые равны по 70° и являются друг для друга вертикальными.
Что и требовалось доказать.
Точка пересечения диагоналей квадрата является центром квадрата. Т.к. из него проведена перпендикулярная прямая, значит расстояние от т. О до вершин квадрата будет одинаковое. Следовательно, нам нужно найти одно такое расстояние, чтобы знать все.
Стороны квадрата (а) равны. Диагонали у квадрата равные (d), и точк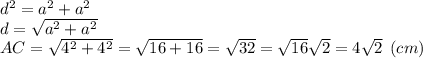 а пересечения делит их пополам.
а пересечения делит их пополам.
Р-м ΔAOM:
∠O = 90°, AO — половина диагонали, OM — перпендикуляр к плоскости квадрата. АМ — наклонная.
AO = d/2
Ищем, чему равна диагональ квадрата:
AO = (4√2)/2 = 2√2 см
Теперь можем найти длину отрезка AM
ответ: Расстояние равно √33 см, или приблизительно 5,74 см.