Биссектриса прямого угла прямоугольного треугольника делит гипотенузу на отрезки длиной 3см 4см. Найдите радиус круга, вписанного в треугольник
Объяснение:
Пусть один катет а, другой катет b. . По т. о биссектрисе треугольника
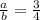, тогда а= 
.
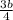По т. Пифагора а²+b²=(3+4)² ,( 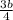)²+b²=49 ,
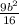+b²=49 , 9b²+16b²=49*16 , b²= 
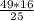, b=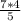
= 5,6 (см)
a=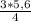 
=4,2 cм
S=1/2*Р*r . Найдем площадь прямоугольного треугольника
S=1/2*5,6*4,2=1/2*23,52 (см²) . Найдем периметр Р=16,8 см. Тогда
1/2*23,52=1/2*16,8*r , r= 23,52/16,8 , r=1,4 см
===============================
Теорема о биссектрисе треугольника " Биссектриса треугольника делит противоположную сторону на два отрезка, длины которых относятся так же, как длины соответствующих сторон."
прямые ,проходящие через середину большей стороны
значит одна сторона разделена на две части
противоположная большая сторона на три части
равновеликие части - значит площади равны у всех ТРЕх частей
площадь параллелограмма
S=a*h < длина большей стороны -a высота -h
тогда площадь каждой части S/3
одна часть точно треугольник, потому что вершина упирается в середину большей стороны
площадь треугольника S/3 = 1/2 *x*h <х - основание треугольника
S/3= a*h /3 = 1/2 *x*h
x=2/3 a <-- одна часть найдена
две другие части - трапеции с основаниями a/2 и y
площадь трапеции S/3 = 1/2 *(a/2+y)*h <y - основание трапеции
S/3= a*h /3 = 1/2 *(a/2+y)*h
a /3 = 1/2 *(a/2+y)
a*2 /3 = (a/2+y)
a*2 /3 -a/2 =y
y = a*2 /3 -a/2 = a (2/3 - 1/2) = a/6
ОТВЕТ
вторую сторону прямые делят на отрезки 1/6 ; 2/3 ; 1/6
равновеликие части : треугольник, 2 трапеции