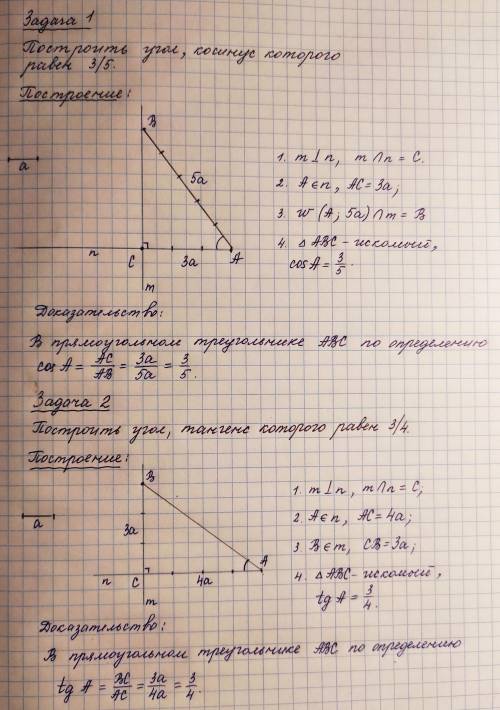
Задачи на построение в прикреплённом изображении.
3) sin α = 15/17;
cos α = 8/15;
tg α = 1 7/8.
Объяснение:
Задача 3.
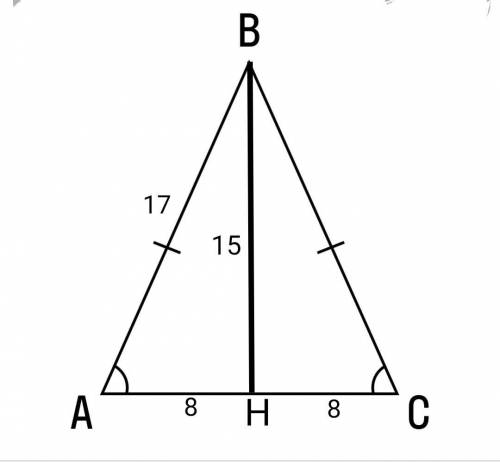
1) Обозначим данный треугольник АВС. По условию АВ = ВС = 17 см, основание АС = 16 см.
Пусть ВН - медиана, проведённая к основанию, по свойству равнобедренного треугольника она является высотой, тогда
АН = НС = 16 : 2 = 8 (см) и ∠ АНВ = 90°.
2) В прямоугольном треугольнике АВН по теореме Пифагора
АВ² = АН² + ВН²
ВН² = АВ² - АН² = 17² - 8² = 289 - 64 = 225,
ВН = √225 = 15 (см).
3) По определению в ∆АВН
sin A = ВН/АВ = 15/17;
cos A = AH/AB = 8/15;
tg A = BH/AH = 15/8 = 1 7/8.
АБ = БС = 14, АС = 26 , углол С = А = 24, угол Б = 132.
Объяснение:
треугольник АБС, где угол Б = 132 градуса, С = 24, а сторона противолежащая углу С = 14 см.
по теореме синусов составляем пропорцию:
с / син 24 = б /син132
14 / 0,407 = б / 0,743
(числа взяты из таблицы синусов)
б = 14 * 0.743 / 0.407 = 25.557
26см получилась сторона АС.
угол С равен 24, а угол Б = 132, исходя из этого можем посчитать третий угол т.к. сума внутренних углов треугольника всегда равна 180
132+24= 156, а 180-156=24
следовательно второй угол при основе 24. угол А = 24 и угол С = 24, значит треугольник ривнобедренний (сори не знаю как на русском), а это значит, что сторона с = а
если что, спрашивай
ролджпагщщбмагщдмпшзбмр