Высота делит прямой угол на 2+1=3 части. каждая по 90°:3=30°.
Меньшая часть= 30°, большая =60°
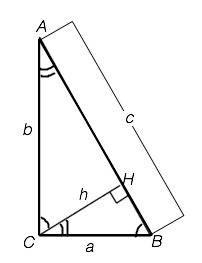
Высота прямоугольного треугольника к гипотенузе делит его на треугольники, подобные друг другу и исходному.
⇒ в ∆ АВС угол А=30° (см.рисунок).
Примем меньший катет равным а, он противолежит углу 30°, поэтому гипотенуза равна 2а ( свойство).
Второй катет АС=2а•cos30°=a√3
Площадь прямоугольного треугольника равна половине произведения катетов.
S=a•b:2
2S=a•а√3
4√3=a²√3⇒
a²=4,⇒ a=2
S (АВС)=AB•h:2
h=2S:2a=4√3:4=√3
Пусть SABCD -правильная пирамида.Квадрат-основание правильной пирамиды.
SO⊥(ABCD) , SO=4. Cоединим точки А и С. ∠SAO=45°. Найдём из Δ ASO катет АО :tg∠ASO=SO/AO ⇒
AO=SO·tg45°=4·1=4/ AO=4
AO=1/2 АС ⇒ АС=2·АО = 2·4=8 Диагональ квадрата АВСD =8.
Из Δ АСD по т. Пифагора АС²=AD²+DC². ПУСТь AD=DC=x
Тогда 8²=2х² ⇒ х√2=8 ⇒х=8/√2 =4·√2
S(осн)=х²=(4·√2)²=16·2=32
V=1/3·S(осн)·H =1 /3· 32 ·4=128/3