========================================================
Периметр правильного треугольника, вписанного в окружность, равен 45 см. Найдите сторону правильного восьмиугольника, вписанного в ту же окружность.
========================================================
AB = a = 45 : 3 = 15 смРадиус окружности, описанной около правильного треугольника, вычисляется через его сторону: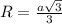
Радиус окружности, описанной около правильного восьмиугольника, вычисляется через его сторону:
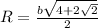Приравниваем правые части и находим искомую величину:
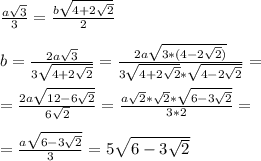b - сторона правильного шестиугольника b ≈ 6,63 смОТВЕТ: 5√(6 - 3√2)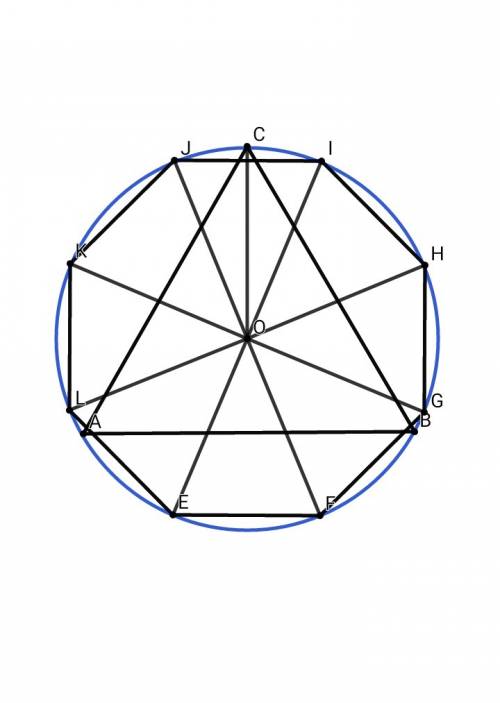 
Достроим треугольник до параллелограмма, так, что бы медиана стала половиной диагонали. Пксть треугольник АВС медиана ВО Продолжим медиану на такое же расстояние Получим отрезок ОД. Тогда параллелограмм АВСД Сумма квадратов диагоналей параллелограмма равна сумме квадратов его сторон получим 2ВА*ВА+2 ВС*ВС = ВД*ВД +АС*АС 2*27*27+2*29*29= 52*52+х*х 1458+1682=2704+х*х 1340=2704+х*х х*х= 436 х= 2 корня из 109 .Из вершины С поведём высоту это СР СР*СР=29*29-у*у СР*СР= 436-(27-у)*(27-у) 841-у*у= 436-729+54у-у*у 54у=1134 у=21 У это ВК, где К основание высоты , а 27- у это АК Найдём высоту КС КС*КС=29*29-21*21 =400 КС=20 см.
Вектор АВ + вектор АС= вектор 0, якщо вектори протилежнi. У них спiльний початок точка А, вони розташованi на однiй прямiй. Точка А у цьому випадку середня точка вiдрiзки ВС.
В (4; -2; 12), С (3; -1; 4) за умовою, тодi А( (4+3)/2; (- 2-1)/2; (12+4)/2),
А(3,5; -1,5; 8)