Теорема о секущих :
если из точки, лежащей вне окружности, проведены две секущие, то произведение одной секущей на её внешнюю часть равно произведению другой секущей на её внешнюю часть.
Примем коэффициент пропорциональности отрезков стороны параллелограмма за х.
Тогда получаем равенство 9х*7х = 21*3 = 63,
63х² = 63,
х² = 1,
х = √1 = 1.
Получаем длину стороны 9 см.
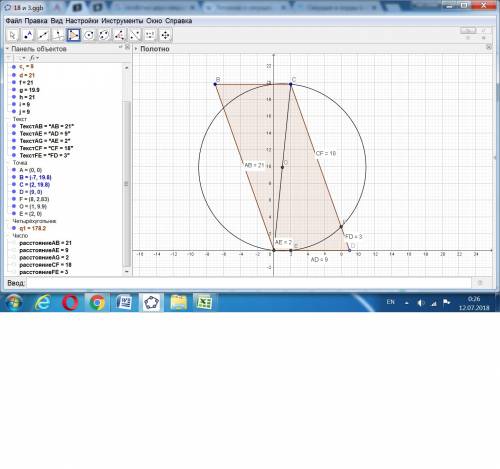
Отрезок СЕ будет высотой параллелограмма, так как АС - диаметр. а угол АЕС - прямой
Высоту находим по Пифагору:
Н = √(21² - 7²) = √(441 - 49) = √392 = 14√2 см.
Отсюда получаем площадь:
S = 9*14√2 = 126√2 ≈ 178,191 см².
sin(BAH)=BH/AB=7/6>1
Синус угла не может быть больше 1, значит такой треугольник невозможен. Значит основание BC=6см, а стороны AB=AC=14см. Для проверки можем найти синус того же угла при новых условиях, он будет равен sin(BAH)=3/14, это допустимое значение. Значит основание треугольника - 6см, а боковые стороны - 14см.