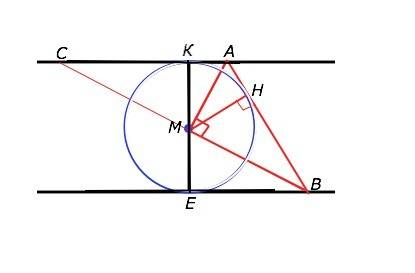
Расстояние между параллельными прямыми есть длина перпендикулярного этим прямым отрезка, заключенного между ними.
Обозначим данные прямые а и b. Отрезок КЕ ⊥ а, КЕ ⊥ b.
М - середина КЕ, КМ=МЕ=50. Угол АМВ=90°.
Продолжим ВМ до пересечения с прямой а в точке С.
∆КМС =∆ВМЕ по катетам КМ=МЕ и вертикальным углам при М. Смежные углы АМВ=АМС=90°,АМ - высота и медиана ∆ САВ, ⇒,
АМ - биссектриса угла ВАС.
Каждая точка биссектрисы равноудалена от сторон угла. МК=МН, где МН - расстояние от М до АВ.
М - центр вписанной в угол САВ окружности с диаметром, равным расстоянию между параллельными а и b.
Наименьшее расстояние от точки до прямой – перпендикуляр, и наименьшим расстоянием от М до АВ будет радиус МН=МК окружности с диаметром КЕ=100, т.е. отрезок, равный половине КЕ:2=50 (ед. длины).
В основании пирамиды лежит правильный треугольник ABC со стороной равной 6см.
S(осн.)= =9√3 см².
=9√3 см².
Высота правильной пирамиды падает в центр основания. Поэтому если DH высота пирамиды, а DM - апофема, то MH - радиус вписанной окружности в правильный треугольник. Т.к. по теореме о 3ёх перпендикулярах HM⊥AC.
В прямоугольном ΔDHM (∠H=90°) найдём гипотенузу DM по теореме Пифагора.
Боковые грани правильной пирамиды это равные треугольники.
S(бок.)= =9√147 см²
=9√147 см²
S(полн.) = S(осн.)+S(бок.) = 9√3 + 9√147 см²
ответ: 9√3 + 9√147 см².