Т.к. АС⊥ВС, МК⊥ВС, то МК║АС, а т.к. ВК/КС=1/2, то и
ВМ/МА=1/2⇒
ВМ=5. /по теорему Фалеса/
Из ΔАВС: АС=√(АВ²-ВС²)=√((10+5)²-(4+8)²)=√(27*3)=9
МК = 3, т.к. ΔВМК - египетский. Значит, искомая площадь -
площадь трапеции МКСА равна (МК+АС)*КС=(3+9)*8/2=12*4=48/см кв./
Поскольку площадь основания равна 16 см2, то сторона призмы = 4 см.
B1D - диагональ призмы, тогда BD - диагональ основы и проекция B1D на основу.
BD=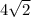
как диагональ основы, которая является квадратом.
Отсюда за теоремой Пифагора с треугоьника BB1D:
B1D=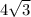
см.
Расстоянием от AA1 до B1D является перпендикуляр.
Проекция этого перпендикуляра - половина BD
Если соеденить концы этих отрезков, то получится прямоугольник. Отсюда следует, что:
MN=BD/2=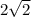
, MN - расстояние между прямыми AA1 и B1D
Сделаем рисунок.
Пусть сторона, к которой прилежат углы, данные в условии, будет основанием АС треугольника АВС.
Из вершины В опустим к АС высоту ВН.
С ее мы отсекли от треугольника АВС равнобедренный прямоугольный треугольник АВН.
Угол ВАС=45° по условию, АВН равен ему - из прямоугольногоо треугольника АВН.
Обозначим катеты ВН и АН этого треугольника х ( т.к. они равны).
Тогда НС=2-х,
а сторона ВС, как гипотенуза треугольника ВНС, в котором, катет противолежащий углу 30°, равен х, равна 2х.
Составим уравнение по теореме Пифагора для стороны ВС треугольника ВНС.
ВС²=НС²+ВН²
(2х)²= х ²+(2-х)²
4х²= х²+ 4-4х+х ²
2х²+ 4х-4 =0
D=b²-4ac=4²-4·2·-4=48
х1= (- 4 +√48) :4= -( 4 - 4√3) :4= -4(1-√3):4=√3-1
ВС=2(√3-1) ≈1,464
АВ=(√3-1)√2=√6-√2≈ 2,449-1,414≈1,035
48 см^2
Объяснение: