
Чтобы узнать, существует ли такой треугольник со сторонам 3; 3; 8 — надо сравнить каждую сторону с суммой друх других сторон: 8+3 = 11.
Каждая сумма двух сторон должна быть больше каждой стороны, чтобы такой треугольник существовал.
Сумма боковый сторон — 3+3 = 6, которая меньше стороны 8, тоесть треугольник со сторонами 3; 3; 8 — не существует.
Теперь представим, что боковые стороны равны 8; 8, а основание — 3.
3+8 = 11 > 3;
8+8 = 16 > 3
8+3 = 11 > 3.
В этом случае, треугольник сущестует, а основание — 3, боковые стороны — 8; 8.
ответ: 11
Объяснение:
Так как ABCD параллелограмм, то BC || AD ⇒ ордината точки C совпадает с ординатой точки B (равной 8)
Пусть абсцисса точки C равна x, тогда C имеет координаты (x; 8)
По формуле расстояния между точками составим уравнение для A и C:
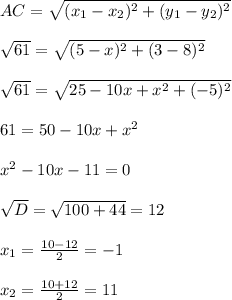
Так как ABCD параллелограмм, то BC = AD = 3 ⇒ абсцисса точки B меньше на 3, чем абсцисса точки C. Чтобы ∠ BAD был острым, нужно, чтобы абсцисса точки B была больше абсциссы точки А.
На основе найденных x, найдём абсциссы точки B:
При x = -1: -1 - 3 = -4 < 5 -- угол тупой (не подходит)
При x = 11: 11 - 3 = 8 > 5 -- угол острый