а) По определению проекция фигуры на плоскость - совокупность проекций всех точек этой фигуры на плоскость проекции.
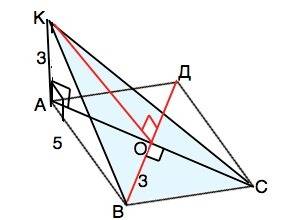
Точка К проецируется в основание перпендикуляра КА, т.е. в т. А.
Т. В и С ∆ КВС лежат в плоскости ромба. Через две точки можно провести только одну прямую. ⇒
Все точки сторон ∆ КВС проецируются на стороны ∆ АВС. ⇒
∆ АВС проекция ∆ КВС на плоскость ромба АВCД.
б) КА перпендикулярен плоскости ромба, следовательно, перпендикулярен любой прямой, проходящей в этой плоскости через т. А. ⇒КА⊥АС
Диагонали ромба взаимно перпендикулярны.⇒АС⊥ВД
АО - высота равнобедренного ∆ АВД. Из ∆ АОВ по т.Пифагора АО=√(B²-BO²)=√(25-9)=4
Расстояние от точки до прямой равно длине проведенного между ними перпендикуляра.
КО по т. о 3-х перпендикулярах перпендикулярен ВД.
Из прямоугольного ∆ КАО расстояние КО=√(КА²+АО*)=√(9+16)=5 см
По теореме, сумма внутренних углов треугольника равна 180°. Значит,
1) С=180°-(А+В)=180°-(50°+60°)=180°-110°=70°;
2) Е - прямой угол, значит равен 90°, F=180°-(E+D)=180°-(90°+20°)=180°-110°=70°;
3) по свойству равнобедренного треугольника (MK=ML по условию) K=L, K+L=180°-M=180°-40°=140°, K=L=140°:2=70°;
5) по свойству равнобедренного треугольника (AB=CB по условию) А=С, В - прямой угол, значит равен 90°, А+С=180°-В=180°-90°=90°, А=С=90°:2=45°.
Объяснение:
по теореме о сумме углов треугольника и свойству равнобедренного треугольника.