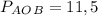 см
см
∠AOB=90°
∠ABO=50°
∠BAO=40°
Объяснение:
Дано: ABCD - ромб
CD = 3 см
AC = 9 см
BD = 8 см
∠C = 80°
Найти: PΔ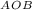 = ?
= ?
∠AOB=?
∠ABO=?
∠BAO=?
Решение: т.к ABCD - ромб, то у него все стороны равны ⇒ CD=BC=AB=AD=3 см
Диагонали ромба точкой пересечения делятся пополам: BO=OD=8/2=4 см; AO=OC=9/2=4,5 см
Противолежащие углы ромба равны ⇒ ∠C=∠A=80°, но т.к диагонали ромба являются биссектрисами его углов, то ∠OAD=∠BAO=80/2=40°
Диагонали ромба пересекаются под прямым углом ⇒ ∠AOB=90°
В ΔABO - прямоугольном, найдем ∠ABO. Сумма острых углов в прямоугольном треугольнике = 90°
∠ABO+∠BAO=90; ∠ABO=90-∠BAO; ∠ABO=90-40; ∠ABO=50°
Периметр - сумма длин всех сторон, тогда 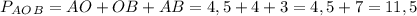 см
см
меньший катет АС=6см, больший катет ВС=12√3 см
Объяснение:
обозначим вершины треугольника А В С с прямым углом С катетами АС и ВС и гипотенузой АВ. Проекции катетов на гипотенузу образует высота СН проведённая из вершины прямого угла, поэтому СН перпендикулярно АВ. СН также делит ∆АВС на 2 прямоугольных треугольника АСН и СВН в которых АН, ВН, СН - катеты, а АС и ВС - гипотенузы. Он подобны между собой, так как высота проведённая из вершины прямого угла делит его на прямоугольные треугольники подобные между собой и каждый из них подобен ∆АВС. АВ=АН+ВН=6+18=24 см. Рассмотрим ∆АСН и ∆АВС. В ∆АСН АС является гипотенузой, а в ∆АВС - гипотенуза АВ, поэтому гипотенуза АС~ гипотенузе АВ. А также меньший катет ∆АСН АН~ АС(меньшему катету ∆АВС:
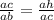
теперь подставим наши значения в эту пропорцию:
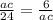
перемножим числитель и знаменатель соседних дробей между собой крест накрест и получим:
АС ²=6×24=144
АС=√144=12см
Теперь найдём катет ВС по теореме Пифагора:
ВС²=АВ²–АС²=24²–12²=576–144=432=12√3см

16см
Объяснение:
Пусть коэффициент пропорциональности равен х.
Тогда периметр шестиугольника (сумма шести сторон) равен
2х+3х+5х+5х+4х+3х = 22х = 176 см. => х = 8см.
Меньшая из сторон равна 2х = 16см.