12
Объяснение:BD - наибольшая диагональ = 12√3.
<A = 120.
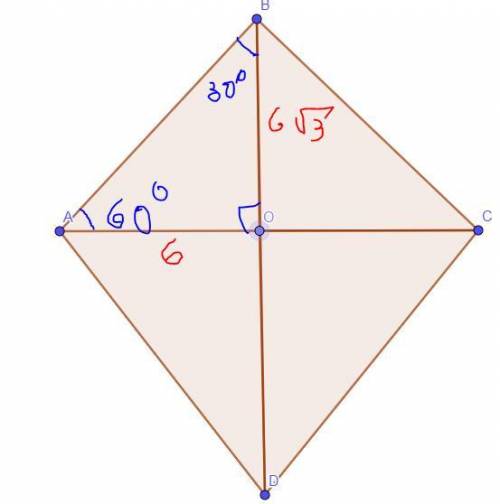
1) Посколько диагонали ромба одновременно перпедикулярны (т.е. создают 4 угла по 90°) и являются биссектрисами углов, то меньшая биссектриса AC разбивает <A на 60°.
Из треугольника ABO, нам известно, что <O = 90°. Не сложно найти тогда и <B:
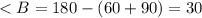 °.
°.
2) DB = 2OB, посколько диагонали ромба точкой сечения делятся пополам, т.е OB = 6√3
Из треугольника ABO найдём сторону AO, лично мне будет удобно использовать теорему синусов, кто-то может использовать тригонометрические соотношения углов, как вам удобно. Итак, имеем:
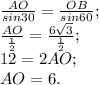
3) AC = 2AO, посколько диагонали ромба точкой сечения делятся пополам, т.е:
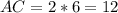 - значения наименьшей диагонали.
- значения наименьшей диагонали.
В прямоугольном треугольнике АВН , АВ равна 13, так как sinA=12/13, тогда по теореме Пифагора АН=√13^2-12^2 = 5
В прямоугольном треугольнике ВНС , ВН/ВС=4/5
12/ВС=4/5
ВС=15
тогда НС=√15^2-12^2= 9
Тогда АС=5+9=14 . По теореме синусов
15/12/13=2R
13*15/24 = R
R=8.125
Длина окружности
L=2*pi*8.125 = 16.25 pi
2) Я вычислил уже стороны они равны 15;14;13
по формуле Герона
p=(15+14+13)/2=21
S=√21*6*7*8 = 84
ответ 84
3) Найдем длину самой биссектрисы
так как
тогда по теореме косинусов , отрезок первый
тогда второй