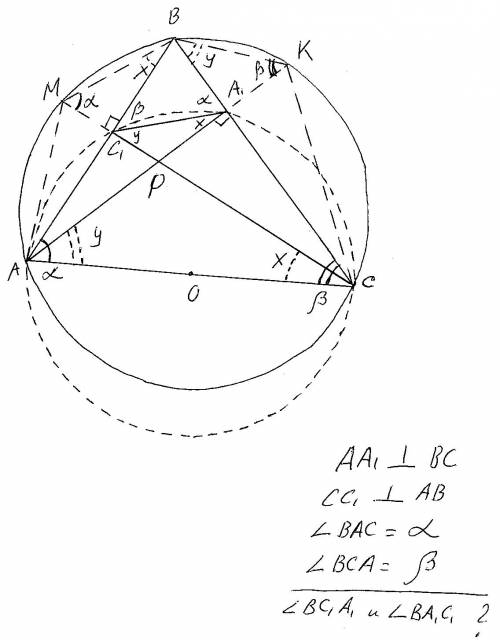
Обозначим треугльник АВС(смотри рисунок). Проведём высоты АА1 и СС1. Треугольники АС1С и АА1С прямоугольные и гипотенуза АС у них общая. Известно, что центр О описанной окружности лежит на середине гипоенузы. В данном случае нам важно то, что вокруг указанных треугольников может быть описана одна общая окружность, которая будет также описанной окружностью для четырёхугольника АС1А1С. А далее смотрим дуги и углы на которые они опираются. Вписанные углы опирающиеся на одну и ту же дугу равны. Например угол ВКА=углу ВСА=бетта. Поскольку они опираются на дугу АМВ, далее в решени приводятся равные углы и дуги на которые они опираются . Затем из прямоугольных треугольников МВС1 и ВА1К находим значения углов Х и У, подставляем и получаем угол ВА1С1=альфа, угол ВС1А1=бетта.
дано:
треуг. абс равносторонний. т.е
аб=вс=ас
угол а = углуб = углу с = 60 град.
бм - биссектриса.
найти аб, вс, ас
равносторонний треугольник будет и равнобедренным, тогда биссектриса будет медианой и высотой.
биссектриса бм разобьёт треугольник абс на 2 равных прямоугольных треугольника (абм и всм) в треугольнике авм ам = 1/2 аб ( можно использовать 1 из вариантов 1. бм - медиана в равностороннем треугольнике. 2.угол абм = 30 градусов)
так как треугольник абм прямоугольный то по теореме пифагора найдём аб
аб - гипотенуза ам - катет = 1/2 аб вм катет равный 2^3 = 8
пусть аб - х
тогда х^2= (1/2x)^2 + 8^2
x^2 - 025x^2=64
0,75x^2=64
x^2= 64/0.75 ~ 85
x= sqrt(85)
если под 2^3 имелось в виду 2sqrt(3)то
x^2=0,25x^2+12
0,75x^2=12
x^2=16
x=4
sqrt - это квадратный корень.