Построение сводится к проведению перпендикуляра из точки к прямой.
Из вершины А, как из центра, раствором циркуля, равным АС, делаем насечку на стороне ВС. Обозначим эту точку К.
∆ КАС- равнобедренный с равными сторонами АК=АС.
Разделив КС пополам, получим точку М, в которой медиана ∆ КАС пересекается с основанием КС. Т.к. в равнобедренном треугольнике медиана=биссектриса=высота, отрезок АМ будет искомой высотой.
Для этого из точек К и С, как из центра, одним и тем же раствором циркуля ( больше половины КС) проведем две полуокружности. Соединим точки их пересечения с А.
Отрезок АМ разделил КС пополам и является искомой высотой ∆ АВС из вершины угла А.
Отрезок АВ разделён на 5 равных частей. Найдите координаты точек С и Е, если А ( 1; 2; 6), В(0; 10; 15) .
Объяснение:
1) Для точки С имеем λ=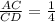
=0,25 .
x(C)=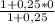
=1:1,25=0,8 ,
у(C)=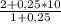
=4,5:1,25=3,6 ,
z(C)=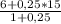
=9,75:1,25=76,8 . Значит С( 0,25 ; 3,6 ; 7,8)
2) Для точки Е имеем λ=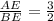
=1,5 .
x(E)=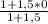
=1: 2,5=0,4 , у(E)= 
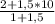=17 : 2,5=6,8
z(E)=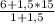
=9,75: 2,5=11,4 Значит С( 0,4 ; 6,8 ; 11,4) .
========================
х=(х₁+λх₂):(1+λ) ,у=( у₁+λу₂):(1+λ) ,где (х₁;у₁), (х₂;у ₂) -координаты концов отрезка , (х;у)-координаты точки, делящей отрезок в заданном отношении.