15° 75°
Объяснение:
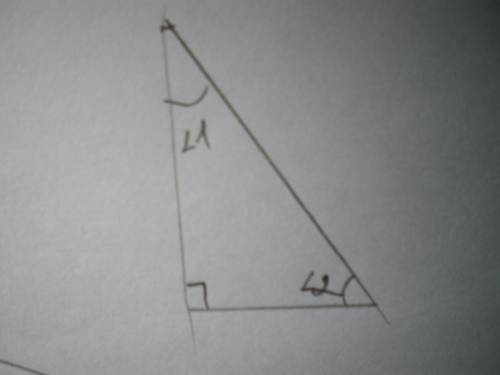
Сумма острых углов прямоугольного треугольника составляет 90°. Пусть ∠1=х°, тогда ∠2=5х°.
х+5х=90
6х=90
х=15°
∠1=15°, ∠2=15*5=75°
пусть в треугольнике АВС угол С-прямой, АА1иСС!-биссектрисы, АА1 пересекает СС1 в точке О. биссектриса делит угол пополам поэтому угол АСС1=углу ВСС1=45градусов. По условию угол АОС1=70градусов. угол АОС1-внешний к треугольнику АСО. По свойству он равен сумме внутренних углов не смежных с ним, 45 градусов + угол САО=70градусов, угол САО=70градусов - 45градусов=25градусов, АА1-биссектриса, значит угол САА1=углу ВАА1=25градусов, угол А=25градусов+25градусов=50градусов, сумма острых углов прямоугольного треугольника = 90 градусов, поэтому угол В= 90градусов -50градусов=40градусов
ответ 50градусов и 40градусов
1 угол =15
2 угол = 15*5=75
Объяснение:
Пусть 1 угол = х градусов
2 угол = 5х градусов
90+5х+х=180
6х=90
х=15
1 угол =15
2 угол = 15*5=75