Объяснение:
Основная формулировка содержит алгебраические действия — в прямоугольном треугольнике, длины катетов которого равны {\displaystyle a}a и {\displaystyle b}b, а длина гипотенузы — {\displaystyle c}c, выполнено соотношение:
{\displaystyle a^{2}+b^{2}=c^{2}}a^{2}+b^{2}=c^{2}.
Возможна и эквивалентная геометрическая формулировка, прибегающая к понятию площади фигуры: в прямоугольном треугольнике площадь квадрата, построенного на гипотенузе, равна сумме площадей квадратов, построенных на катетах. В таком виде теорема сформулирована в Началах Евклида.
Обратная теорема Пифагора — утверждение о прямоугольности всякого треугольника, длины сторон которого связаны соотношением {\displaystyle a^{2}+b^{2}=c^{2}}a^{2}+b^{2}=c^{2}. Как следствие, для всякой тройки положительных чисел {\displaystyle a}a, {\displaystyle b}b и {\displaystyle c}c, такой, что {\displaystyle a^{2}+b^{2}=c^{2}}a^{2}+b^{2}=c^{2}, существует прямоугольный треугольник с катетами {\displaystyle a}a и {\displaystyle b}b и гипотенузой {\displaystyle c}c.
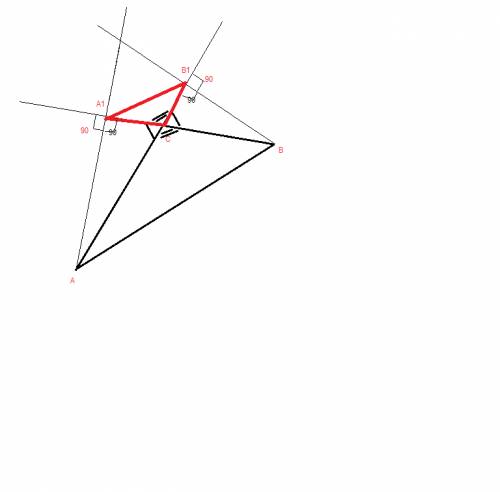
Доказать подобие треугольников А1СВ1 и АВС.
сделаем построение по условию
треугольники ACA1 и ВСВ1 - подобные по ПЕРВОМУ признаку подобия (по двум углам)
<AA1C=<BB1C=90 град
<ACA1=<BCB1 -вертикальные
следовательно , соответственные стороны относятся
СA1 / CB1 =CA / CB = k1 -коэффициент подобия для треугольников ACA1 и ВСВ1
отношение можно записать по-другому
СA1 / CA = CB1 / CB = k2 -коэффициент подобия для треугольников А1СВ1 и АВС.
т.е. треугольники А1СВ1 и АВС подобны по ВТОРОМУ признаку подобия
(если две стороны одного треугольника пропорциональны двум сторонам другого треугольника и углы между этими сторонами равны)
пропорциональные стороны СA1 / CA = CB1 / CB
<A1CB1 = <ACB --вертикальные
доказано подобие треугольников А1СВ1 и АВС.
S