1) 116
2) 62°
3) 416
1) Биссектриса равностороннего треугольника совпадает с медианой и высотой.
Обозначим а - сторона,
h - высота. Равносторонний треугольник равны все стороны и равны углы, причем углы равны 60°.
Рассмотрим треугольник образованный стороной высотой (биссектрисой)
и третьей стороной будет часть стороны на которую опущен треугольник. Рассматриваемый треугольник прямоугольный. И углы соответсвенно равны 90° , 60° и 30°.
Справедливо: а=h/cos30°. a=58×2=116.
2) Величина угла ACB, равна половине угла AOB, который равен 124°. Угол ACB=(124°/2)=
62°.
3)
BC=2×MC; AC=2×NC.
MC=(1/2)×BC; NC=(1/2)×AC
S(ABC)=1/2×AC×BC×sinC,
S(MNC)=1/2×MC×NC×sinC,
Отсюда S(ABC)=4×S(MNC)=4×104
S(ABC)=416
Площадь трапеции находится по формуле
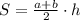
где a, b -- основания трапеции, h -- высота.
h = 10 см, S = 240 см² по условию
Пусть меньшее основание равно x см, тогда большее равно (x + 4) см.
Составим уравнение, используя формулу площади трапеции:
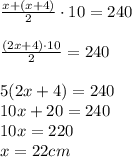
Таким образом, меньшее основание BC равно 22 см, а большее AD равно (22+4) = 26 см.
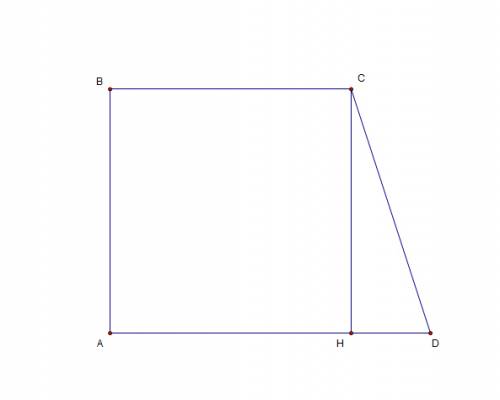
В прямоугольной трапеции одна из боковых сторон равна высоте, то есть AB = 10 см.
Проведём из точки С высоту CH. Тогда HD = AD - BC = 26 - 22 = 4 см
CH = h = 10 см. По теореме Пифагора найдём CD:
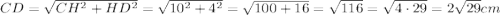
ответ: 10 см, 22 см, 26 см, 2√29 см
1) 60/13
2) АD=13
3) 60√3
4) 120/13
Объяснение:
ABCD-ромб⇒АС⊥ВD, АО=0,5АС, DО=0,5ВD
АО=0,5АС=0,5·10=5
DО=0,5ВD=0,5·24=12
АС⊥ВD, по теореме Пифагора АD²=АО²+DО²=5²+12²=25+144=169⇒АD=13
2) АВ=ВС=СD=АD=13-сторона ромба
3) Площадь орт.проекции фигуры на плоскость равна произведению площади данной фигуры на косинус угла между плоскостью и данной фигурой.
Площадь ромба по готовой формуле: S=0,5AC·BD=0,5·10·24=120
Площадь орт проекции: s=S·cos((ABCD)∧α)=120·cos30°=120·√3/2=60√3
4) Через точку О - пересечение диагоналей ромба проведём перпендикуляр к стороне ВС, OM⊥BC.
Но так как ВС║AD⇒ME⊥AD, ME⊥BC⇒ME-высота ромба.
Ещё одна формула для нахождения площади ромба
S=ME·AD⇒120=ME·AD=13ME⇒ME=120/13
1) Опустим из точки М перпедикуляр МТ на плоскость α.
МТ⊥α, Е∈α⇒отрезок TE есть орт.проекция отрезка МЕ на плоскости α.
АD⊥МЕ⇒АD⊥ТЕ(теорема о трёх перпендикулярах)
Значить, ∠МЕT=(АВСD∧α)=30°
МТ⊥α, ЕТ∈α⇒МТ⊥ ЕТ⇒∠МТЕ=90°
∠МТЕ=90°,∠МЕT=30°⇒MT=0,5ME=0,5 ·120/13=60/13
Растояние между ВD и пл.α и есть отрезок МТ=60/13
Р.S. Все 4 пункта вычислены. Соответствие это выбор подходящего варианта ответа
1-В
2-А
3-Б
4-Д