Объяснение:
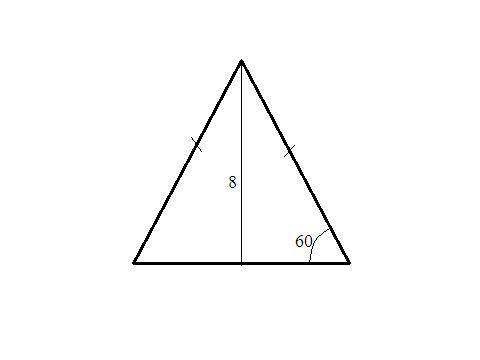
Осевое сечение конуса - равнобедренный треугольник с боковыми сторонами (образующие конуса), основание - диаметр основания.
Треугольник, образованный высотой, образующей и половиной диаметра - прямоугольный. Угол при вершине (90-60)=30° ⇒ половина диаметра (катет против угла 30°) равен половине образующей (гипотенуза). По т. Пифагора -
(2х)²=8²+х²
х²=8²/3
х=8/√3;
Площадь - S=a*h/2, где а=2х=16/√3, h=8;
S=16*8/(2√3)=64/√3=64√3/3.
Можно проще.
Угол при основании 60° ⇒ треугольник равносторонний.
S=h²/√3=8²/√3=64/√3=64√3/3.
Объяснение:
Прямая, параллельная стороне АС треугольника АВС, пересекает его сторону АВ в точке М, а сторону ВС - в точке К. Найдите площадь треугольника АВС, если АМ = 4 см, АС = 8 см, АМ = МК, а площадь треугольника МВК равна 5 см2.
ответ: 20 см²
Объяснение: МК║АС, АВ- секущая, ВС - секущая. Соответственные углы при пересечении параллельных прямых секущей равны, ⇒ ∆ АВС~∆ МВК. По условию МК=АМ=4, АС=8, ⇒ k=AC:МК=8:4=2.
Отношение площадей подобных фигур равно квадрату коэффициента подобия. S(АВС):S(МВК)=k²=2²=4
S(АВС)=S(МВК)•4=5•4=20 см²