0,2
Объяснение:
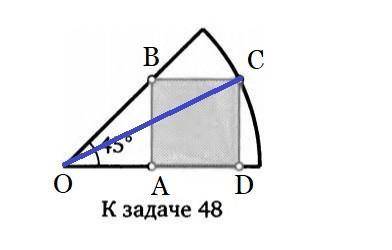
ΔOAB - прямоугольный, <BOA = 45°, ⇒ <ABO = 90° - 45° = 45°, ⇒ ΔOAB - равнобедренный, ⇒ OA = OB.
Пусть AB = x, тогда AD = x = CD, т.к. ABCD - квадрат.
Построим отрезок OC, OC - радиус по построению, т.к. О - центр окружности, а точка C лежит на окружности, ⇒ OC = 1.
Рассмотрим прямоугольный ΔODC: OD = OA + AD = x + x = 2x, CD = x, тогда по теореме Пифагора OC² = OD² + CD² , получаем уравнение:
1² = (2x)² + x²
1 = 4x² + x²
5x² = 1
x² = 1/5 = 0,2
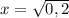 - сторона квадрата, тогда площадь квадрата x² = 0,2
- сторона квадрата, тогда площадь квадрата x² = 0,2
0,2
Объяснение:
ΔOAB - прямоугольный, <BOA = 45°, ⇒ <ABO = 90° - 45° = 45°, ⇒ ΔOAB - равнобедренный, ⇒ OA = OB.
Пусть AB = x, тогда AD = x = CD, т.к. ABCD - квадрат.
Построим отрезок OC, OC - радиус по построению, т.к. О - центр окружности, а точка C лежит на окружности, ⇒ OC = 1.
Рассмотрим прямоугольный ΔODC: OD = OA + AD = x + x = 2x, CD = x, тогда по теореме Пифагора OC² = OD² + CD² , получаем уравнение:
1² = (2x)² + x²
1 = 4x² + x²
5x² = 1
x² = 1/5 = 0,2
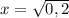 - сторона квадрата, тогда площадь квадрата x² = 0,2
- сторона квадрата, тогда площадь квадрата x² = 0,2

∠BСD = 30°
Объяснение:
В ромбе диагонали являются биссектрисами. =>
∠ABC = 2·∠ABD = 2·75 = 150°.
Углы ромба, прилежащие к одной стороне, в сумме равны 180°.
Следовательно, ∠BСD = 180° - 150° = 30°