Диаметр окружности: отрезок  .
.
Центр окружности: точка 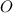 .
.
Координаты следующих точек: 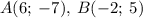 .
.
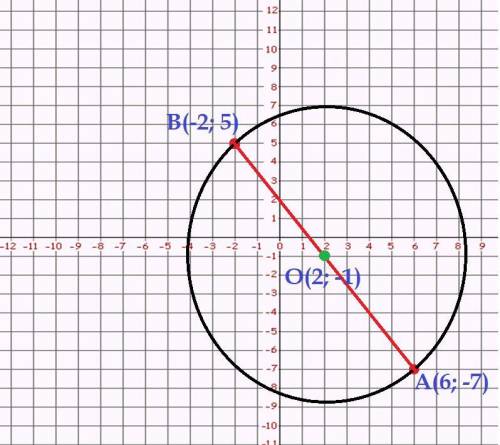
Найти нужно координаты центра окружности:  .
.
Найдём координаты центра окружности, используя правило нахождения среднего арифметического чисел.
Т.е. возьмём у точки "A" и точки "B" координату по оси абсцисс (Ox). Представьте, что мы должны найти среднее арифметическое чисел "6" и "-2".
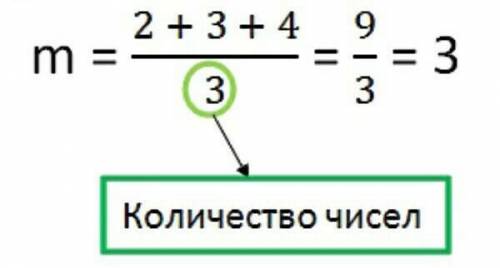
Вспоминаем правило: чтобы найти среднее арифметическое, нужно сложить все числа и поделить их сумму на их количество (пример прикреплён ниже).
Теперь поработаем с выбранными координатами точек:
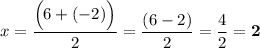 .
.
Теперь мы знаем, что за координата указана по оси абсцисс. Но нам ещё нужно найти координату по оси ординат (Oy).
Делаем всё по аналогии нахождения координаты оси абсцисс. Берём вторые координаты у обоих точек, которые образуют отрезок "AB". Это будут координаты "-7" и "5". Теперь находим их среднее арифметическое и получаем ответ:
 .
.
(чертёж к задаче прикреплён ниже)
ответ: .
. 
1)
Сумма углов в треугольнике равна 180°, можем найти третий угол
∠A=180-(∠C+∠B)=180-150=30°
По свойству прямоугольного треугольника, сторона, лежащая против угла 30° равна половине гипотенузы, значит сторона ВС=1/2 * 16/2=8см
2)*Видимо, Вы тут ошиблись в условии, не может из угла С идти высота BD, его заменю на СD*
Cумма углов треугольника равна 180 градусам, можем найти третий угол
∠B=180-(∠C+∠A)=180-110=70°
Теперь, поскольку CD - высота, то треугольник BCD - прямоугольный, откуда
∠CBD + ∠CDB + ∠BCD = 180°
70 + 90 + ∠BCD =180°
∠BCD =20°
чертежи сам начерти, а я словами напишу:
3. Т.к. сумма углов треугольника всегда = 180°, то
∠A + ∠B + ∠C = 180°, ∠B = 60°, ∠C = 40°,
тогда ∠A = 180° - 60° - 40° = 80°,
т.к. AD - биссектриса, то ∠CAD = ∠BAD = ∠A/2 = 80°/2 = 40°,
Рассмотрим треугольник CAD, в нём ∠С = ∠CAD = 40°, и поэтому по известной теореме треугольник CAD равнобедренный, то есть AD=CD.
б) Рассмотрим треугольник ABD, против большего угла в треугольнике лежит большая сторона, поэтому AD > BD, но AD = CD, поэтому CD > BD.
4. Т.к. треугольник равнобедренный, то неизвестная сторона равна либо 5 см, либо 12 см. Но 5 см не годится, поскольку при этом не выполняется неравенство треугольника (сумма длин любых двух сторон треугольника всегда больше длины третьей стороны). 5 см + 5см = 10 см < 12 см. (неравенство треугольника не выполняется). Если же неизвестная сторона = 12 см, то неравенство треугольника выполняется.
ответ. 12 см.
5. Расстояние от т. K до прямой MN - это длина перпендикуляра, опущенного из этой точки на эту прямую. Проведем этот перпендикуляр KH.
∠N = 180° - ∠K - ∠M = 180° - 90° - 60° = 30°.
Рассмотрим прямоугольный треугольник KNH. Используем теорему: в прямоугольном треугольнике катет, лежащий против угла в 30°, равен половине гипотенузы, то есть KH = KN/2 = 32,6дм/2 = 16,3 дм.
ответ. 16,3 дм.