α = 45°
Объяснение:
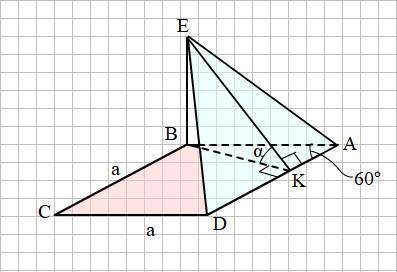
Смотри прикреплённый рисунок.
Из вершины В ромба проводим высоту ВК.
ВК = а · sin A = a · sin 60° = 0.5a√3.
Соединим точку Е с точкой К. ВК является проекцией наклонной ЕК на плоскость АВСD. Поскольку ВК - высота ромба. то ВК ⊥ AD.
По теореме о трёх перпендикулярах: если AD ⊥ BK (проекции наклонной ЕК), то AD⊥ ЕК. Следовательно, ∠ЕКВ = α является линейным углом, служащим мерой двугранного угла между плоскостями ADE и АВСD.
Найдём этот угол.
tg α = BE : BK = 0.5a√3 : 0.5a√3 = 1.
Следовательно, ∠α = 45°
Радиус = 16
Объяснение:
И так начнём с формулы для радиуса. R= abc/(4*S)
Т.к. сумма углов треугольника = 180, а в равнобедренном треугольнике углы при основании равны, находим их:
(180-120)=30
Проводим высоту(она же медиана) и получаем два равных прямоугольных треугольника с гипотенузой 8 и углом 30;
Сторона которая лежит напротив угла 30 равна половине гипотенузы=>
Высота равнобедренного треугольника равна 4. Через cos(30) находим второй катет. sqrt(3)/2 = x/8=> x=2sqrt(3)
Находим основание . треугольника= 2sqrt(3)*2=4 sqrt(3)
Площадь же равна = (a*b*sin(120))/2 = 32*sin120= 32sqrt(3)/2
Подставляем всё в самую первую формулу
R= 8*8*4sqrt(3)/(32 sqrt(3)/2). Корень с трех сокращается и просто считаем. ответ 16