Эту задачу можно решить двумя .
1) Геометрический.
Так как плоскость отсекает на осях равные отрезки, то углы между осями и плоскостью равны.
Для примера возьмём угол к оси Oz.
Угол между прямой и плоскостью равен плоскому углу между этой прямой и её проекцией на плоскость.
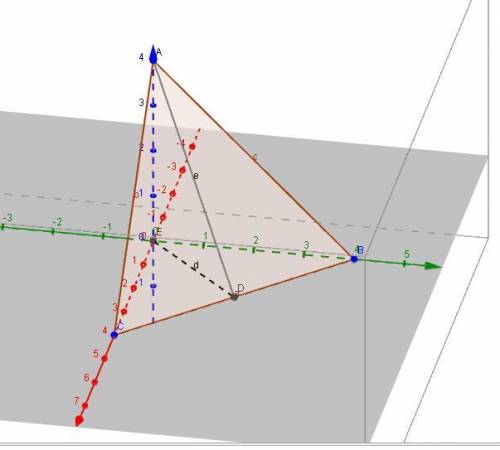
Проекция оси Oz на плоскость лежит на прямой АД.
ОД = 4*cos 45 = 4*(√2/2) = 2√2.
Угол α = arc tg (2√2/4) = arc tg(√2/2) = 35,264 градуса.
2) Векторный.
Уравнение плоскости "в отрезках" (x/4) + (y/4) + (z/4) = 1.
В общем виде x + y + z - 4 = 0.
Направляющий вектор плоскости N = (1; 1; 1), его модуль равен √3.
Косинус угла между направляющим вектором плоскости и осью Oz равен: cos β = 1/√3. Сам угол равен arc cos(1/√3) = 54,7356 градуса.
Угол между нормалью к плоскости (прямой ее содержащей) и осями в сумме с искомым углом дают 90 градусов.
Тогда α = 90 - β = 90 - 54,7356 = 35,2644 градуса.

Так как треугольник АВС - прямоугольный, а угол А=60 градусов, то угол В равен 180 - 90 - 60 = 30 градусов.
Катет, лежащий напротив угла 30 градусов равен половине гипотенузы, следовательно, так как ВА(гипотенуза)=8 м, то АС = 4 м.
Найдём второй катет (ВС) по теореме Пифагора:
ВС = √ВА² - АС²
ВС = √64 - 16
ВС = √48
ВС = 4√3
ответ: 4√3 м.