Пусть дана равнобокая трапеция ABCD, у котрой MN - средняя линия, АС и BD - диагонали, являющиеся биссектрисами острых углов. Пусть средняя линия пересекает диагональ АС в точке К и МК=8 см, KN=12 см. МК является средней линией треугольника АВС, то по свойству средней линии треугольника ВС=2*МК=16 см. KN является средней линией треугольника BCD, то по тому же свойству AD=2*KN=24см. Треугольник АВС равнобедренный, т. к. угол ВАС равен углу DAC, т.к. Ас - биссектриса угла А, а угол DAC= углу ВСА как внутренние накрест лежащие при ВСIIAD и секущей АС, следует угол ВАС= углу АСВ и АВ=ВС=16 см, а т.к. данная трапеция равнобокая, то CD тоже = 16 см.З=3*16+24=72 см
ответ: 72 см
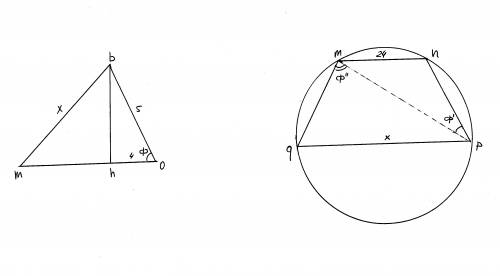
1). см левый рисунок на чертеже.
По теореме синусов x = 2*R*sin(Ф); sin(Ф) вычисляется из треугольника bho, который, очевидно, "египетский" (3,4,5) :))) то есть sin(Ф) = 3/5; x = 2*10*3/5 = 12;
2). см. правый рисунок на чертеже.
Я отметил углы, которые принял за заданные: sin(Ф') = 0,2; cos(Ф") = 0,6; (конечно, таким я себе жизнь облегчил, но тут уж все - к автору задачи :)))
Имеем cos(Ф") = 0,6; откуда sin(Ф") = 0,8;
Поскольку у треугольников mqp и mnp общая описанная окружность, из теоремы синусов следует
x/0,8 = 24/0,2;
отсюда x = 96, а средняя линяя равна (96 + 24)/2 = 60;
Объяснение:
напротив угла в 30° лежит катет который равняется половине гипотенузы