1. Сторона треугольника a= 2Rcos30o.
2. 1) Знайдемо радіус вписаного кола у правильний трикутник:
2) Діагональ вписаного у коло квадрата рівна діаметру цього кола і дорівнює подвоєному радіусу:
3) Сторону квадрату знайдемо за т. Піфагора:
3.
4.В трапецию можно вписать окружность, если сумма противоположных сторон равна. то есть AD+BC=AB+CD
Опустим с вершины B трапеции на основание BK высоту BK, тогда
AK=AD-KD=28-21=7
Пусть высота трапеции BK=x, тогда
(AB)^2=(BK)^2+(AK)^2=x^2+7^2
AB=sqrt(x^2+7^2)
Так как
AD+BC=AB+CD, то
21+28=x+sqrt(x^2+7^2)
sqrt(x^2+7^2)=49-x
x^2+7^2=(49-x)^2
x^2+49=2401-98x+x^2
98x=2352
x=24, то есть высота трапеции равна 24
R=H/2
R=24/2=12 - радиус вписанной окружности
ответ: 16 (ед. объёма)
Подробное объяснение:
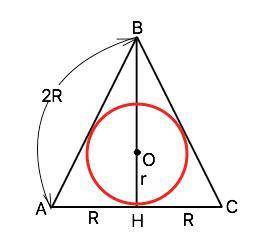
Схематический рисунок осевого сечения шара, вписанного в конус – окружность с радиусом r (радиус шара), вписанная в треугольник АВС. В данной задаче треугольник АВС правильный, его сторона равна диаметру основания конуса. ⇒ АВ=ВС=АС=d=2R
Высота ВН треугольника АВС – высота конуса ВН=АВ•sin60°=2R•√3/2=R√3. Подставим значение высоты в формулу объёма конуса:
V(к)=πR²•h/3= πR²•R√3/3=πR³/√3 ⇒ πR³/√3=36
Радиус r окружности, вписанной в правильный треугольник, равен 1/3 высоты этого треугольника ( высоты конуса). r=OH=(R√3):3=R/√3
Подставим найденное значение радиуса шара в формулу его объёма:
V(ш)=4π(R/√3)³/3=4πR³/9√3
Из найденного объёма конуса πR³/√3=36
подставим это значение в выражение объёма шара:
V(ш)=4•36/9=16 (ед. объёма)
Відповідь:
Пояснення: