Цилиндр описан около сферы.
R цилиндра = 2 см.
Найти:S полн поверхности цилиндра - S полностью поверхности сферы = ?
Решение:Так как в данный цилиндр вписана сфера, по условию ⇒ D сферы = h цилиндра.
R цилиндра = R сферы = 2 см (так как в цилиндр вписана сфера).
⇒ D сферы = h цилиндра = R сферы * 2 = 2 * 2 = 4 см.
S полн поверхности цилиндра = 2πR(R + h), где R - радиус цилиндра; h - высота цилиндра.
S полн поверхности цилиндра = π(2 * 2(2 + 4) = 24π см²
S полной поверхности сферы = 2πR² , где R - радиус сферы.
S полной поверхности сферы = π(4 * 2²) = 16π см²
⇒S полн поверхности цилиндра - S полн поверхности сферы = 24 - 16 = 8π см²
ответ: 8π см²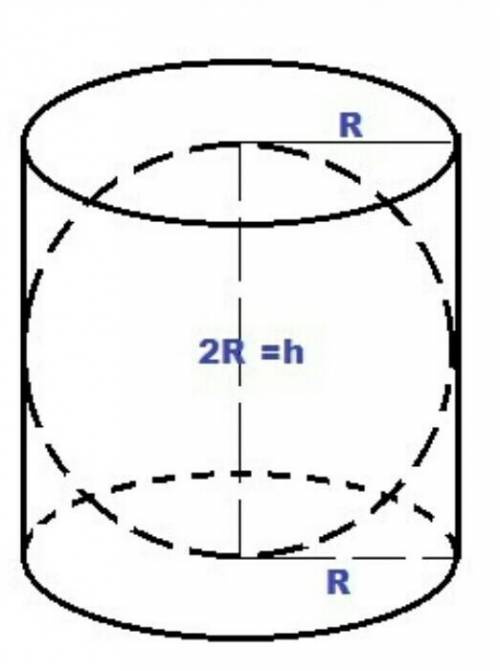
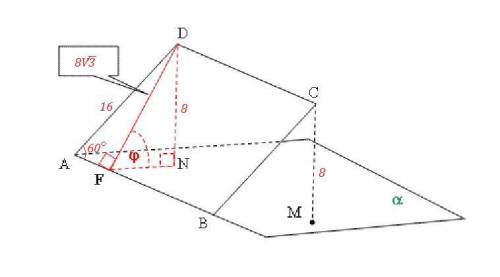
ABCD - ромб , AD=16 , ∠А=60° , АВ ∈ пл.α
Проведём DN ⊥ пл.α , DN - расстояние от точкиD до пл.α , DN=8 .
1. CD║AB как противоположные стороны ромба, AB⊂пл. α ⇒ CD║пл.α . Все точки CD равноудалены от пл.α, значит расстояние от точки С до пл. α равно расстоянию от точки D до пл. α . CM⊥пл. α , СМ=8 .
2. Проведём DF ⊥ AB и рассм. ΔАDF . DF=AD*sinA=16*√3/2=8√3 .
DN⊥пл. α , DF⊥AB , значит FN - проекция DF на пл.α и по теореме о трёх перпендикулярах FN⊥AB . Тогда линейным углом двугранного угла между ромбом и плоскостью α будет угол DFN .
Рассм. ΔDNF. DN ⊥ FN , DN=8 , sin∠DFN=DN/DF=8/8√3=1/√3 .
Если же не ∠А=60°, а ∠В=60°, то рассуждения аналогичны.
CM=DN=8 по тем же соображениям.
Проводим CF⊥AB, получаем ΔCBF, откуда находим CF=8√3.
Линейным углом двугранного угла между ромбом и пл.α будет ∠CFM . Из ΔCFM находим sin∠CFM=1/√3 .
Координаты вектора равны разности соответствующих координат точек его конца и начала. Тогда вектор АВ = (Xb-Xa;Yb-Ya;Zb-Za).
AB(1;-1;-5)
BC(-2;-2;1).
Умножение вектора на число: p*a=(pXa;pYa;pZa), где p - любое число.
2*AB(2;-2;-10).
3*BC(-6;-6;3).
Сложение векторов : a+b=(x1+x2;y1+y2;z1+z2)
Вектор (2*AB+3BC) = (-4;-8;-7).