ответ: NM= 10см
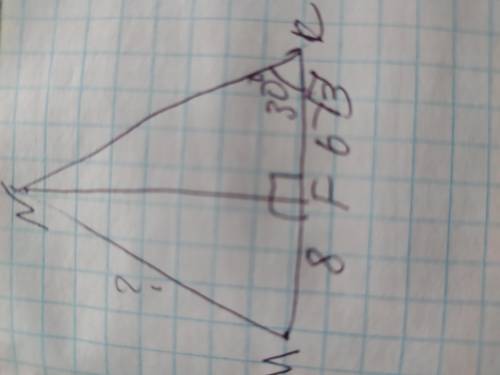
Объяснение: высота NF делит ∆ MNK на два прямоугольных треугольника в которых высота NF является катетом. Рассмотрим полученный ∆NKF. По условиям угол NKF составляет 30°, а катет, который лежит напротив этого угла равен половине гипотенузы. Пусть катет NF будет х, тогда гипотенуза NK будет 2х. Составим уравнение и найдём стороны ∆MKF по теореме Пифагора:
NF²+FK²=NK²
x²+(6√3)²=(2x)²
x²+36×3=4x²
x²+108=4x²
x²-4x²= - 108
- 3x²= - 108
3x²=108
x²=108÷3
x²=36
x=6; сторона NF=6см, тогда гипотенуза NK будет 6×2=12см
Теперь найдём искомую сторону NM по теореме Пифагора, зная MF и NF:
NM²=MF²+NF²
NM=8²+6²=√(64+36)=√100=10см
NM=10см
ответ: Р=42см
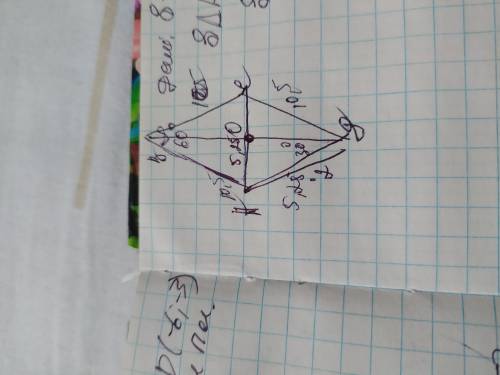
Объяснение: проведём вторую диагональ ВД. Пусть точкой их пересечения будет точка О. Так как диагонали ромба, пересекаясь делятся пополам, образуют прямой угол и делят углы пополам, то АО=ОС=½×АС=10,5÷2=5,25см. Рассмотрим ∆АВО. В нём угол АОВ=90°(его образуют диагонали. Зная, что угол В=60°, то угол АВО= 60÷2=30°. В этом треугольнике АОВ, катет АО лежит напротив угла 30°, а значит равен половине гипотенузы АВ. АВ=5,25×2=10,5см. Теперь найдём периметр ромба, зная его сторону:
Р=10,5×4=42см; Р=42см
Дано: АВС - трикутник, АВ=ВС=2√13 см, ВН=6 см. Знайти S(АВС).
S=1\2 * АС * ВН.
Розглянемо ΔАВН - прямокутний. За теоремою Піфагора,
АН²=АВ²-ВН²=52-36=16; АН=4 см.
АС=2АН=8 см.
S=1\2 * 8 * 6 = 24 см²
Відповідь: 24 см²