Опускаем перпендикуляр BH к AD.Рассмотрим треугольник АВН.в нем:
угол АНВ=90,угол ВАН=45 угол АВН=180-(90+45)=45.
соsВ=ВН/АВ √2/2=ВН/4; ВН=(4*√2)/2=2√2
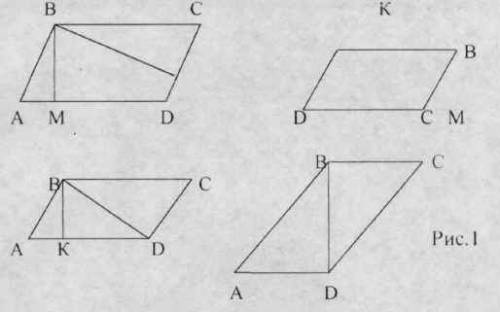
первый рисунок
рассмотрим треугольник АВМ угол а 45 гр. угол ВМА 90гр.
отсюда угол АВМ=180-90-45=45
треугольник АВМ равнобедренный АМ=ВМ
16=АМ^2+ВМ^2
АМ=ВМ=корень из8= 2 корень из 2
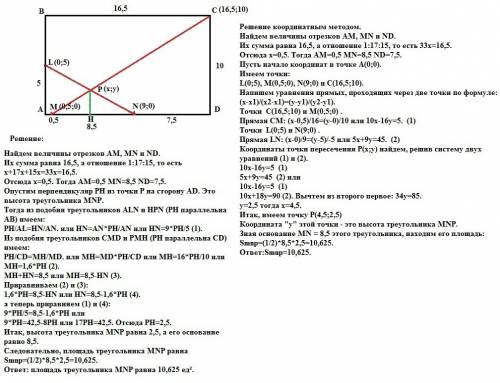
1. Пусть одна сторона параллелограмма равна х см, а вторая у см. Тогда периметр параллелограмма будет равен 2х+2у=48 см, но по условию известно что х-у=7 см.
Решим полученную систему уравнений:
2х+2у=48
х-у=7 |*2 (умножим второе уравнение на 2);
2х+2у=48 (сложим полученные уравнения)
+
2х-2у=14;
2х+2х+2у-2у=48+14
4х=62
х=62/4
х=15,5
Найдем у:
х-у=7
15,5-у=7
-у=7-15,5
у=8,5
ответ: Стороны параллелограмма равны 15,5 см и 8,5 см.
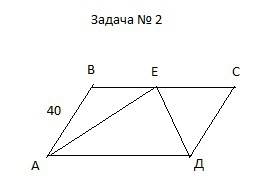
2. АВ=СД (так как АВСД – параллелограмм)
Свойство биссектрисы параллелограмма:
Биссектриса параллелограмма отсекает равнобедренный треугольник
Значит АВ=ВЕ=40 см. и СД=СЕ=40 см.
ВС=ВЕ+СЕ=40+40=80 см.
высота будет равна 4*sin45=4*(√2)/2=2√2