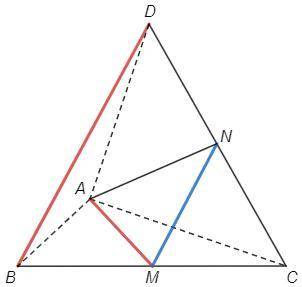
В правильном тетраэдре ABCD точка M - середина BС. Найдите угол между прямыми AM и BD.
Прямая BD пересекает плоскость (ABC) в точке, не лежащей на прямой AM - прямые AM и BD скрещиваются.
Угол между скрещивающимися прямыми - угол между параллельными им пересекающимися прямыми.
Проведем MN||BD
∠AMN - искомый угол.
Правильный тетраэдр, все грани - правильные треугольники.
Пусть все ребра равны а
N - середина CD (т Фалеса)
MN=a/2 (средняя линия)
AM=AN =a√3/2 (медианы в равностороннем треугольнике)
△MAN - равнобедренный
cos(AMN) =MN/2AM =2a/4a√3 =√3/6
∠AMN =arccos(√3/6)
` ` — Здравствуйте, Norfsakilla! ` `
• Объяснение:
— | Чтобы правильно решить данную задачу, нужно быть очень умным и внимательным. | —
• Решение:
— | А теперь, давайте приступим к решению данной задаче. Начнём с 4-го и до 1-го. | —
• Фигура Nō⁴ : У фигуры номер ⁴ нет равных пар треугольников, потому что они не совпадают из за овалов, которые находятся в самом нижнем углу.
• Фигура Nō³ : У фигуры номер ³ нет равных пар треугольников из-за тех же овалов, которые находятся в нижнем углу.
• Фигура Nō² : Многие могут подумать, что правильным ответом будет считаться Фигура номер ², но они глубоко ошибаются, потому что у второй пары треугольника нет маленького квадратика в нижнем углу, который есть у первой пары треугольника, и также, это сто процентов никто не заметил, но я заметила : у второй пары треугольника, где нет квадратика, на букве М есть рядом маленькая и незаметная точечка. Приглядитесь.
• Фигура Nō¹ : А вот фигура номер ¹ может считаться правильным ответом, потому что квадратики, точечки и маленькие полосочки по серединке совпадают.
— | А теперь, когда мы разобрали данную задачу и нашли правильный ответ, мы можем записать его. | —
• ответ: у фигуры Nō¹ пары треугольников равны.
` ` — С уважением, EvaTheQueen! ` `
6
Объяснение:
аₙ=(( n-2) /n) *180°, где n количество сторон, аₙ -угол.
120°=((n-2) /n) *180°
120n=180n-360
60n=360
n=360/60=6 сторон