Обозначим стороны параллелограмма за a и b, высоты за hᵃ и hᵇ, и:
a = 30 см, hᵃ = 12 см, hᵇ = 18 см.
Формула площади параллелограмма:
S = a·hᵃ, a — сторона параллелограмма, hᵃ — высота, опущенная на сторону a.
Подставим значения и найдем площадь данного параллелограмма:
S = 30·12 = 360 (см²)
Воспользуемся формулой площади для нахождения второй стороны параллелограмма:
S = b·hᵇ ⇒ b = S/hᵇ
b = 360/18 = 20 (см)
ответ: Другая сторона параллелограмма равна 20 см.

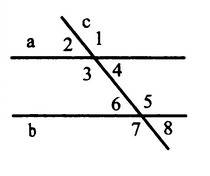
При пересечении двух параллельных прямых третьей (не под прямым углом) образуются 8 углов, четыре из которых имеют одну величину и четыре - другую:
На рисунке видны такие углы 1 и 3; 2 и 4, а так же 5 и 7; 6 и 8. Очевидно, что все эти пары представляют собой равные углы, так как являются вертикальными. Таким образом, мы имеем четыре бо'льших угла: 1, 3, 5, 7 и четыре меньших: 2, 4, 6, 8. Разность между бо'льшим и меньшим углом, по условию, равна 44°. Сумма большего и меньшего равна 180°. Тогда:
{ ∠1 - ∠2 = 44°
{ ∠1 + ∠2 = 180° - Складываем оба уравнения:
2 *∠1 = 224° => ∠1 = 112°; ∠2 = 180 - 112 = 68°
Таким образом: ∠1 = ∠3 = ∠5 = ∠7 = 112°
∠2 = ∠4 = ∠6 = ∠8 = 68°
Это решается через площадь.
Пусть первая сторона - a1, вторая сторона- a2. Первая высота - h1, вторая - h2.
В первом случае площадь параллелограмма равна a1 * h1
Во втором случае - a2 * h2
Площадь равна 12 * 30 = 360см^2
Подставляем во второй случай:
360= h2 * a2
Выражаем a2 : 360/18 = 20 см
Надеюсь, это лучший ответ)