Объяснение:
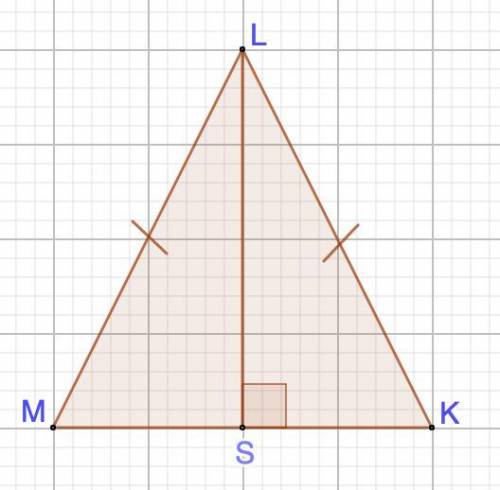
Дано: ΔLMK - равнобедренный.
МК - основание.
LS - высота
Доказать: ΔLSM = ΔLSK, используя 2 и 3 признаки равенства треугольников.
Доказательство:
1) 2 признак равенства треугольников:
Если сторона и два прилежащих к ней угла одного треугольника соответственно равны стороне и двум прилежащим к ней углам другого треугольника, то такие треугольники называются равными.
Рассмотрим ΔLSM и ΔLSK - прямоугольные (LS - высота)
⇒ ∠LSM = ∠LSK = 90°
В равнобедренном треугольнике высота является биссектрисой.
⇒ ∠MLS = ∠SLK
LS - общая
⇒ ΔLSM = ΔLSK (по 2 признаку)
2) 3 признак равенства треугольников:
Если три стороны одного треугольника соответственно равны трем сторонам другого треугольника, то такие треугольники называются равными.
Рассмотрим ΔLSM и ΔLSK - прямоугольные (LS - высота)
В равнобедренном треугольнике высота является медианой.
⇒ MS = SK
ML = LK (ΔLMK - равнобедренный)
LS - общая
⇒ ΔLSM = ΔLSK (по 3 признаку)
Малюнок у файлах.
Объяснение:
1. Перш за усе, малюємо лінію (червона), може бути якого захочеш розміру.
2. На ній встановлюемо точку А
3. У точку А ставимо циркуль, та робимо коло (фіолетовий), якого хочеш розміру, але не більш лініі з п.1
4. Там, де коло перетинає червону лінію з п.1, точка Б, туди ставимо циркуль.
5. Ставимо циркуль так, щоб гостра ніжка була у точці Б, а олівець у А, малюемо друге коло (синє).
6. У третій точці перетину, між синім та фіолетовим колом, ставимо третю точку В.
7. З'єднуємо три точки
А - Б, вже з'єднані,
А - В, малюємо лінію (помаранчева)
В - Б, малюємо ще одну лінію (помаранчева).
Трикутник з рівними сторонами побудован.
Усi стороны - рiвнi радiуси АВ = АС и ВС = АС

ответ: 60 градусов
Объяснение:
Пусть ∪BC = x градусов, тогда ∪AB = 3x, ∪AC = 2x. В окружности всего 360°. Составим и решим уравнение:
3x + x + 2x = 360°
6x = 360°
x = 60°
Значит, ∪AC = 2 * 60 = 120°, тогда, по свойству вписанных углов, ∠ABC = 1/2 ∪AC = 120/2 = 60°