1. В треугольнике ABC ∠A = 90°, BC = 25 см, AC = 15 см. Найдите: 1) cos C; 2) ctg B.
2. Найдите катет BC прямоугольного треугольника ABC (∠C = 90°), если AC = 8 см, tg A = 1
3. Найдите значение выражения cos2 42° + sin2 42° + sin2 30°.
4. В прямоугольной трапеции KDMT (DM || KT, ∠D = 90°) DM = 6 см, KT = 21 см, MT = 20 см. Найдите синус, косинус, тангенс и котангенс угла T трапеции.
5. Высота NE треугольника FNP делит его сторону FP на отрезки FE и PE. Найдите сторону NF, если EP = 8 см, NP = 17 см, ∠F = 60°.
6. Диагональ равнобокой трапеции перпендикулярна боковой стороне, а угол между боковой стороной и высотой трапеции равен α. Найдите радиус окружности, описанной около трапеции, если её высота равна h.
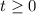
Дано:
ABCD - равнобедренная трапеция, угол A = углу D = 30 градусов, BH и CK - высоты, AB = CD = 58 (см). AD || BC, BC = 16 (см), AD = 96 (см).
Найти: AC.
Решение:
1.Проведём высоты BH и CK, следовательно найдём AH
AH = (AD-BC)/2 = (96 - 16) /2 = 80/2=40 (см).
2. С прямоугольного треугольника ABH (угол AHB = 90градусов):
AH = 40 (см), AB = 58 (см), угол А =30градусов.
Определяем высоту BH.
За т. Пифагора
AB² = AH² + BH²
BH² = AB² - AH²
3. Определяем Диагональ АС.
С прямоугольного треугольника ACK (угол AKC = 90градусов)
За т. Пифагора
ответ: AC = 70 (см).