АВС АС=b, AB=BC=a, AN
ДАЛЬШЕ ПО СА ДЕЙСТВУЕШЬ!
Основание высоты правильной пирамиды проецируется в центр описанной вокруг основания пирамиды окружности.
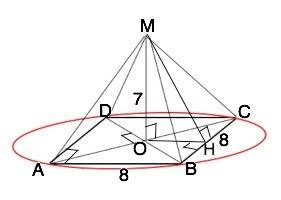
Обозначим пирамиду МАВСD, МО - высота, О - центр описанной окружности= точка пересечения диагоналей квадрата.
АС =8√2 ( по формуле диагонали квадрата).
МО перпендикулярна основан, ⇒ перпендикулярна каждой прямой, проходящей в плоскости АВСD через О.
∆ МОС - прямоугольный.
OC=4√2
По т.Пифагора МС=√(MO²+CO*)=√(49+32)=9
Площадь боковой поверхности пирамиды равна сумме площадей ее граней, которые являются равнобедренными треугольниками,
иначе
Площадь боковой поверхности - произведение апофемы на полупериметр основания.
Высота МН грани ( апофема) является медианой и делит ВС пополам. По т.Пифагора
МН=√(MB²-BH*)=√(81-16)=√65
S=h•MH=16•√65=16√65 (ед. площади)
правильный четрехугольник - это квадрат, центр квадрата, то есть точка пересечения диагоналей и будет центром описанной окружности, потому что удалена от вершин квадрата на одинаковые расстояния, равные половине диагонали. Вот половина диагонали и есть радиус описанной окружности. В данном случае это 6*корень(2)/2, то есть 3*корень(2);
Вообще в квадрате, если известна сторона, то диагональ равна стороне, умноженной на корень из 2. Это следует из теоремы Пифагора, например. :