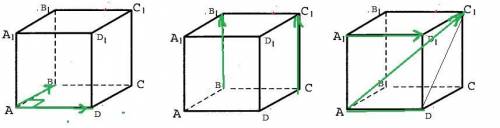
В кубе ABCDA1B1C1D1 найдите угол между векторами:
a)AB и AD , б)BB1 и CC1 , в)AC1 и A1D1
Объяснение:
Углы между векторами а)∠АВ,АD=90°, т.к все грани куба являются квадратами.
б) ∠ВВ₁,СС₁=0°, т.к эти вектора лежат на параллельных прямых.
в) ∠АС₁,А₁D₁=arcctg√2.
Т.к. вектор А₁D₁=AD , то найдем угол ∠АС₁,АD
Из ΔВСС₁ -прямоугольный. Пусть ребро куба а, тогда по т. Пифагора
ВС₁=а√2.
По т. о трех перпендикулярах если проекция ВС перпендикулярна , прямой лежащей в плоскости АВ, то и наклонная С₁В перпендикулярна прямой лежащей в плоскости АВ⇒ ΔАВС₁-прямоугольный .
tg∠С₁FD=BС₁/AB или tg∠С₁FD=а√2/а , tg∠С₁FD=√2 , ∠С₁FD=arctg√2,
а значит у угол между векторами ∠АС₁,А₁D₁=arcctg√2.
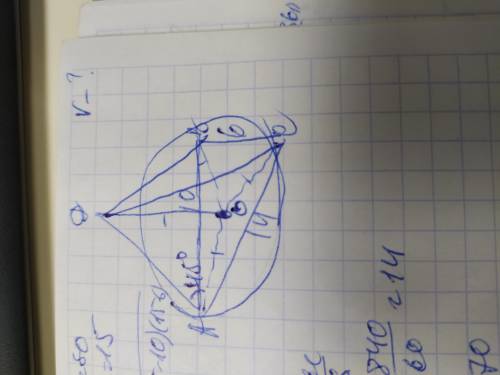
Обозначим вершины пирамиды АВС с высотой ДО. Объем пирамиды вычисляется по формуле: V=⅓×Sосн×ДО. Зная все стороны основания найдём его площадь через его полупериметр:
Р=14+10+6=30; Р/2=p=15дм
S=√((p(p-AC)(p-AB)(p-ВС))=
=√((15(15-14)(15-10)(15-6))=√(15×1×5×9)=
=√225=15дм²
S=15дм²
Опишем вокруг основания окружность с точкой О. АО=ВО=СО=R
R=AB×BC×AC/4S=14×10×6/4×15=840/60=
=14дм
Треугольники образуемые радиусами, высотой ДО и боковыми рёбрами - прямоугольные и так как боковые рёбра образуют с основанием угол 45°, то углы при вершине также будут 45°, поскольку сумма острых углов прямоугольного треугольника составляет 90°, и угол при вершине=90-45=45°, из чего следует что эти треугольники равнобедренные, поэтому радиус R=высоте ДО=14дм.
Теперь найдём объем пирамиды зная её высоту и площадь основания:
V=⅓×15×14=70дм³
ОТВЕТ: V=70дм³
ответ:Скорее тут доказать надо, что они равны между собой.
Объяснение:
Для начала постараемся найти углы треугольника ABC
1) так как стороны AC = CB, треугольник равнобедренный.
2) Угол DCB = 90:2 = 45 , так как высота, проведенная к основанию в равнобедренном треугольнике явл. медианой и биссектрисой.
3) так как углы при основании равны в равнобедренном треугольнике, тогда 180 - 90 = 90, сумма углов A и B.
угол A = углу B = 90:2 = 45 градусам.
Докажем, что треугольник ADC = треугольнику BDC.
1) Угол A = углу B, так как треугольник ABC - равнобедренный.
2) Угол ADC = углу CDB, так как CD - высота.
3) AD = DB - так как CD - высота, медиана и биссектриса равнобедренного треугольника
Следовательно, треугольник ADC = BDC равны по двум углам и стороне