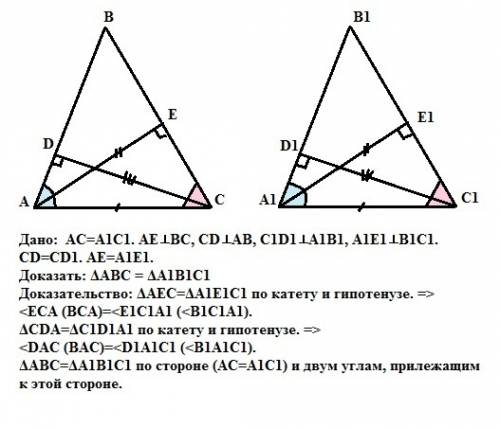
Пусть даны треугольники АВС и А1В1С1, у которых стороны АС и А1С1 равны. Высоты, проведенные из концов этих сторон к боковым сторонам треугольников, также равны. То есть АЕ = А1Е1 и СD = C1D1. Прямоугольные треугольники АЕС и А1Е1С1, ADC и A1D1C1 равны по катету и гипотенузе (четвертый признак равенства прямоугольных треугольников) так как АС=А1С1 (гипотенуза), а АЕ=А1Е1 и CD=C1D1 (катеты) - дано.Из этого равенства следует равенство углов DAC и D1A1C1, а также углов АСЕ И А1С1Е1. Тогда треугольники АВС и А1В1С1 равны по второму признаку равенства треугольников, так как у них равны стороны (АС=А1С1) и углы, прилежащие к этим сторонам (<ВАС = <В1А1С1 и <ВСА=<В1А1С1 - доказано выше).
Что и требовалось доказать.
Основание правильной пирамиды - равносторонний треугольник АВС. Вершина S правильной пирамиды проецируется в т.О – центр правильного треугольника АВС.
Сечение KLM- треугольник.
Искомая площадь S=a•h:2, где a=ML, h=KO
Угол МАL=60°, CL=BM, следовательно, AL=AM ⇒∆ AML – правильный.
АL=AM=9-3=6,⇒ ML=6
Высота основания AH=AB•sin60°=9√3/2=4,5√3
Грани пирамиды - равнобедренные треугольники.
По т.Пифагора из ∆ SHB:
SH²=SB²-BH²=144-20,25=123,75
По т. косинусов вычислим косинус ∠SAH:
SH²=SA²+AH² - 2•SA•HA•cos∠SAH
123,75=144+60,75 - 2•12•4,5√3•cosSAH
-81= -12•9√3•cos∠SAH
Из ∆ KLM по т. косинусов
КО²=КА²+АО²-2•AO•KO•cos∠KAO
КА=SA-SK=12-3=9
AO=2/3 AH=3√3
КО²=81+27 - 2•9•3√3•√3):4
КО²=67,5
КО=1,5√30
S ∆KLM=0.5•6•1,5√30=4,5√30