Центр квадрата - точка О - точка пересечения диагоналей. Диагонали квадрата равны и точкой пересечения делятся пополам: ОА = ОВ. Если проекции наклонных, проведенных из одной точки, равны, то равны и сами наклонные. ОА - проекция МА на плоскость квадрата, ОВ - проекция МВ, значит МА = МВ, т.е. ΔМАВ равнобедренный.
Пусть Н - середина АВ. Так как треугольник МАВ равнобедренный, то МН - его медиана и высота. ОН = 0,5AD = 9 см как средняя линия ΔDAB.
Пусть S₁ - это площадь бо́льшего треугольника, а S₂ - площадь меньшего треугольника.
Пусть k > 1 (это значит, что в числителе будет стоять бо́льший треугольник).
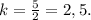
Площади подобных треугольников относятся как квадрат коэффициента подобия.Отсюда -
1,28 (ед²).
- - -
Случай 2 - Площадь меньшего треугольника равна 8 (ед²).В этом случае наоборот k < 1 (в числителе будет стоять меньший треугольник).
S₁ - площадь бо́льшего треугольника, S₂ - площадь меньшего треугольника
Тогда -
50 (ед²).