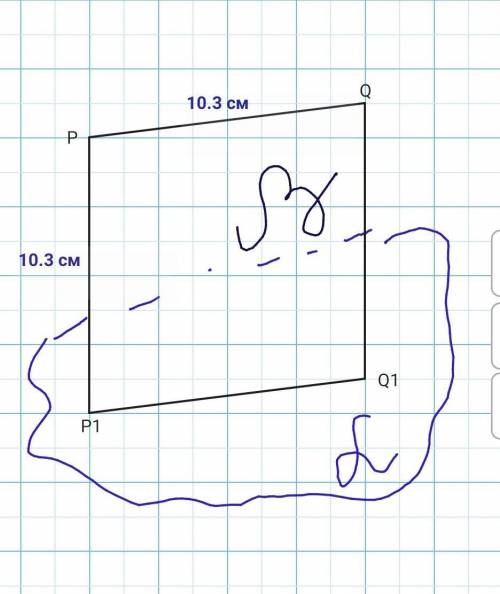
PP1Q1Q-квадрат
Периметр равен 41,2 см
Объяснение:
Две прямые, перпендикулярные одной и той же плоскости, параллельны.PP1 ⊥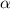 
,
QQ1 ⊥ 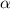=> PP1 II QQ1
PP1 и QQ1 принадлежат одной плоскости B.
Пусть P1Q1 - линия пересечения плоскостей Альфа и Бета.
Если плоскость проходит через прямую, параллельную другой плоскости, и пересекает эту плоскость, то линия пересечения плоскостей параллельна данной прямой.=>PQ II P1Q1
PQQ1P1 - параллелограмм.
Так как < PP1Q1, <QQ1P1 равны 90°, то
PQQ1P1 - прямоугольник.
PP1=PQ => PQQ1P1 - квадрат.
Периметр квадрата находится по формуле:
Р=4а=4×10,3= 41,2 см
Катеты АС и ВС определяются из анализа координат : АС = 6, ВС = 8.
Гипотенуза АВ по Пифагору равна 10.
Величина радиуса вписанной окружности в прямоугольный треугольник:
r = (a+b-c)/2 = (6+8-10)/2 = 4/2 = 2 ед.
Координаты центра находим как среднее арифметическое координат точек (это точка пересечения медиан).
хо = (-6+0+0)/3 = -2,
уо = (0+8+0)/3 = 8/3.
Получаем уравнение окружности:
(x + 2)² + (y - (8/3))² = 2².