Пусть ВА = х, значит АС = 7-х (катеты)
S=0,5·АС·АВ
S=0,5·(7-х)·х
S=х·(3,5-0,5х)
S=3,5х-0,5х²
3,5х-0,5х²=6
-0,5х²+3,5х-6=0
D=3,5²-4·(-0,5)·(-6)=12,25-12=0,25=0,5²
х₁=-3,5-0,5 / -0,5·2 =-4/-1=4
х₂=-3,5+0,5 / -0,5·2=-3/-1=3
ВС²=АВ²+АС² (квадрат гипотенузы равен сумме квадратов катетов)
ВС²=3²+4²
ВС²=9+16
ВС²=25
ВС=5
ответ: гипотенуза равна 5
∠ ВАD = ∠ ВСD = 36°.
∠ АВС = ∠ АDС = 144°.
Пошаговое объяснение:
1. По условию ABCD - параллелограмм. Так как AB = BC, то параллелограмм является ромбом по определению.
2. По свойствам ромба его диагонали взаимно перпендикулярны, тогда ∆ АОD прямоугольный, сумма его острых углов 1 и 2 равна 90°.
3. Пусть ∠ 1 = х°, тогда ∠ 2 = 4х°, получили, что
х + 4х = 90
5х = 90
х = 90 : 5
х = 18
∠ 1 = 18°, ∠ 2 = 18° • 4 = 72°.
4. По свойствам ромба диагонали являются биссектрисами его углов, тогда
∠ ВАD = 2•∠ 1 = 2•18° = 36°.
∠ ВАD = ∠ ВСD = 36°.
5. ∠ АВС = ∠ АDC = 2•72° = 144°.
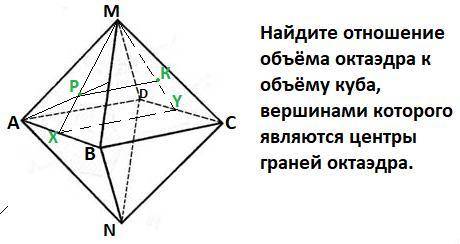
Найдите отношение объёма октаэдра к объёму куба, вершинами которого являются центры граней октаэдра.
Объяснение:
1) Октаэдр это геометрическое тело из восьми граней, каждая их которых - правильный треугольник. Пусть ребро октаэдра а.
V( октаэдра)=1/3*√2*а³ , ABCD-квадрат .
2) Пусть Р-центр правильного ΔАВМ .Тогда М-точка пересечения медиан .Тогда по т. о точке пересечения медиан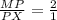 
⇒ 
.
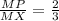3) Аналогично для правильного ΔDCМ ⇒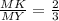 
.
4) ΔМРК подобен ΔМXY по 2-м пропорциональным сторонам ( см п. 2,3) и равному углу между этими сторонами (∠РМК-общий).
Тогда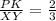 
, 
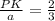,РК= 
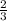*а .
5) V( куба)=( 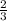*а)³ = 
*а³ . Тогда отношение объёмов будет равно :
= 
.
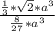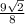a+b = 7 доведем обе части до квадрата.. а^2 +b^2 +2ab = 49 ,а^2 +b^2 = c
с^2 = 49 - 2ab = 49 - 24 = 25 = 5
гипотенуза равна 5 см
"S = ab/2 = 6, ab = 12"