1)
Если трапеция равнобедренная, то АБ=СД=5, следовательно АБ+СД=10.
Тогда сумма двух оснований равна 32-10=22.
Площадь равна средняя линия * h(высоту)
Ср линия = 22/2=11.
Из формулы площади найдем высоту:
h=S/ср.лин
следовательно высота равна 44/11=4
ответ: h=4
2)
S(трапецииABCD) = (AD + BC) : 2 * h
h - высота трапеции и треугольника ACD
S(ACD) = 1/2 * AD * h, следовательно
h = S(ACD) / (1/2 * AD) = 30 / (1/2 * 10) = 30 : 5 = 6 см
S(трапецииABCD) = 1/2*(10 + 8) * 6 = 9 * 6 = 54 см²
P.S. 1/2 - 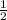
/ - дробь
Площадь описанного круга πR²=49π; R=7
площадь вписанного круга πr²=9π; r=3
Так как ΔABC прямоугольный (a,b - катеты, c - гипотенуза), центр описанного круга совпадает с серединой гипотенузы. c=2R=14
1) SΔABC=(a+b+c)*r/2=a*b/2; (a+b+14)*3/2=a*b/2; 3a+3b-a*b+42=0; a*(b-3)=3b+42; a=3*(b+14)/(b-3);
2) a²+b²=c²; a²+b²=14²; 9*(b+14)²/(b-3)²+(b+14)*(b-14)=0;
9*(b+14)²+(b+14)*(b-14)*(b-3)²=0; b+14 != 0;
9*(b+14)+(b-14)*(b-3)²=0;
9b+126+(b-14)(b²-6b+9)=0; 9b+126+(b³-14b²-6b²+84b+9b-126)=0;
9b+b³-14b²-6b²+84b+9b=0; b!=0;
9+b²-14b-6b+84+9=0;
b²-20b+102=0;
Однако последнее уравнение не имеет действительных корней. Нет ли ошибки в условии?