Pabcd = 24√5
Pabo = 6√5 + 18
∠BCD = ∠BAD ≈ 54°
∠ADC = ∠ABC ≈ 126°
Объяснение:
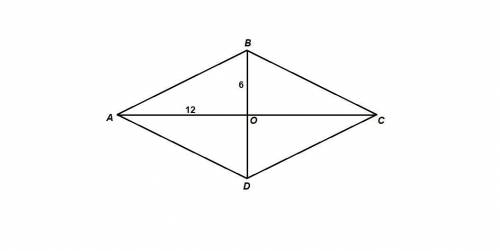
Диагонали ромба перпендикулярны и точкой пересечения делятся пополам, поэтому:
АО = ОС = АС/2 = 24/2 = 12
BO = OD = BD/2 = 12/2 = 6
ΔABO: ∠AOB = 90°, по теореме Пифагора:
АВ = √(АО² + ВО²) = √(12² + 6²) = √(144 + 36) = √180 = 6√5
Pabcd = AB · 4 = 6√5 · 4 = 24√5
Pabo = AB + AO + BO = 6√5 + 12 + 6 = 6√5 + 18
Из прямоугольного треугольника АВО:
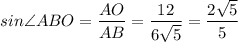
sin∠ABO ≈ 0,8944
∠ABO ≈ 63°
Так как диагонали ромба лежат на биссектрисах его углов, то
∠АВС = 2∠АВО ≈ 126°
Сумма углов, прилежащих к одной стороне параллелограмма, равна 180°, значит
∠BAD = 180° - ∠ABC ≈ 180° - 126° ≈ 54°
Противолежащие углы ромба равны, значит
∠BCD = ∠BAD ≈ 54°
∠ADC = ∠ABC ≈ 126°
В условии задачи, очевидно, ошибка, так как в ромбе с указанными диагоналями нет угла в 60°.
Объяснение:
1)L=(πrα) :180° ,где L– длина дуги,r – радиус окружности, α -центральный угол.
L=π, значит π=(πr*4*α) :180° или 180°=4α или α=45°
2)Пусть одна часть х , тогда ∠КОL-2х, ∠LON=3х, ∠KON=3х.
Получаем 2х+3х+3х=360° или х=45°.
На дугу KN опирается ∠KON=3*45°=135°.
L=(πrα) :180° , L=(π*4*135°) :180°=3π.
,