Две окружности ,вписанные в угол ,касаются друг друга внешним образом .Центральный угол в 120° большей окружности , составленный из радиусов проведенных в точки касания ,стягивает дугу 15 см. Найти длину малой окружности.
Объяснение:
Пусть ОА=ОМ=R , CM=CK=r . По формуле длины дуги ,
⇒ R= см. По свойству отрезков касательных ∠АОР=60° .
Пусть СН⊥ОА , тогда ∠НСО=30°.
В ΔНСО по свойству угла 30° : ОС=2*ОН , но ОС=R+r , ОН=R-r ,
См. рисунки 1) если это параллелогр., тогда уголА=углу С и угол В=углу D рассмотрим треугольник АВК. Он прямоугольный (по условию). АВ=2ВК есть такое св-во- если у прямоугольного треугольника катет равен половине гипотенузы, то он лежит против угла 30 градусов. т.е. угол А (как и С)=30 тогда В=180-30=150 т.е. D=50 2) рассмотрим красные треуг. ВО=ОD, AO=OC (по условию) улы ВОС и АОД равны как вертикальные. значит треуг. равны, соотв. стороны ВС и АД равны. у зеленых треуг. аналогично. А если у четырехугольника противоположные стороны попарно равны, то такой 4-уг явл. параллелограммом (св-во)
Две окружности ,вписанные в угол ,касаются друг друга внешним образом .Центральный угол в 120° большей окружности , составленный из радиусов проведенных в точки касания ,стягивает дугу 15 см. Найти длину малой окружности.
Объяснение:
Пусть ОА=ОМ=R , CM=CK=r . По формуле длины дуги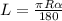
,
Пусть СН⊥ОА , тогда ∠НСО=30°.
В ΔНСО по свойству угла 30° : ОС=2*ОН , но ОС=R+r , ОН=R-r ,
тогда R+r=2(R-r) → r=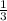
*R → r= 
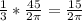(см) .
Длина окружности С=2πr , тогда С=2π*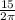
=15 (см) .